- 空间几何体的三视图、表面积和体积
- 共1381题
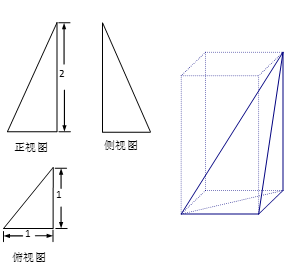
5.高为4的直三棱柱被削去一部分后得到一个几何体，它的直观图和三视图中的侧视图、俯视图如图所示，则该几何体的体积是原直三棱柱的体积的（ ）
A
B
C
D
正确答案
解析
根据三视图可知直观图为：放倒的四棱锥，
∵底面是直角梯形，且上底为4，下底为2，梯高2
∴
∴
又因为
考查方向
解题思路
1）根据直观图形状：放倒的四棱锥，底面是直角梯形，
2）读取几何图形的数据
易错点
主要出现在两个地方：①不能得到直观图为四棱锥，②直观图读取直观图数据错误，特别是底面上的长宽数据
知识点
8.已知一个几何体可切割成一个多面体及一个旋转体的一部分，其三视图如图所示，则该几何体的体积是
A
B
C
D
正确答案
解析
由三视图可得原几何体是由一个半圆柱和一个三棱锥组合而成，圆柱的底面半径为1，高位2，所以体积为
考查方向
解题思路
1)根据几何体的三视图，画出该几何体的直观图；
2)分割几何体，分别判定几何体形状求其体积；
3)求和，即得该几何体的体积。
易错点
本题易在由三视图得到直观图时发生错误，导致体积求错。
知识点
9. 某几何体的三视图如图所示，则该几何体外接球的表面积为 ( )
A
B
C
D
正确答案
解析
画出直观图，如图所示，几何体的外接球即为对应的棱长为1，1，2的长方体的外接球，所以2R=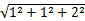
考查方向
解题思路
借助长方体作出几何体的三视图如图所示，几何体的外接球，就是正方体的外接球，可直接算出球的表面积。
易错点
容易将几何体的三视图画错。
知识点
9. 某几何体的三视图如图所示，则该几何体外接球的表面积为 ( )
A
B
C
D
正确答案
解析
画出直观图，如图所示，几何体的外接球即为对应的棱长为1，1，2的长方体的外接球，所以2R=
考查方向
解题思路
借助长方体作出几何体的三视图如图所示，几何体的外接球，就是正方体的外接球，可直接算出球的表面积。
易错点
容易将几何体的三视图画错。
知识点
9．一个空间几何体的三视图如图所示，则这个几何体的表面积为
A
B
C
D
正确答案
解析
由三视图得，几何体为棱长都为
因为三棱锥的四个面全等，所以三棱锥的表面积
A选项不正确，C选项不正确，D选项不正确，所以选B选项。
考查方向
解题思路
由三视图得几何体为多面体；多面体的表面积为各个面面积之和。
易错点
由三视图推导不出原几何体的形状。
知识点
10. 已知一个几何体的三图如图所示，则该几何体的体积为( )
A
B
C
D
正确答案
解析
根据几何体的三视图，可知，立体图形是以高为2，底面积为2的两个集合组合体，根据几何体的体积公式利用底面积乘以高求得，所以选D
考查方向
简单空间图形的三视图
解题思路
本题考查由三视图还原几何体并且看出几何体各个部分的长度，
易错点
空间感不强，还原几何图形时 还原错误
教师点评
本题解题的关键是要求体积需要求出几何体的底面面积和高，三棱锥的高是由垂直与底面的侧面的高得到，本题是一个基础题．
知识点
9.如图，在正四棱柱
A1
B2
C
D
正确答案
解析
由图像可知其正视图的面积是一个定值1，而俯视图显然面积最大为1/2,正视图与俯视图的面积之比的最小值为2,所以选B答案。
考查方向
解题思路
分别找到正视图和俯视图什么时候取到最值然后计算出来。
易错点
不知道什么时候比值最小。
知识点
8．某几何体的三视图如图所示，则该几何体外接球的表面积为（ ）
A
B
C
D
正确答案
解析
由三视图可知，该几何体是底面半径为
考查方向
解题思路
1.先由题中给出的三视图判断出其直观图；2.利用图中给出的数据求其外接球的半径和表面积。
易错点
1.空间想象能力较弱，无法正确判断出其直观图的形状；2.对于几何体与球的切接问题不会处理。
知识点
9. 某几何体的三视图如图所示，则该几何体外接球的表面积为 ( )
A
B
C
D
正确答案
解析
画出直观图，如图所示，几何体的外接球即为对应的棱长为1，1，2的长方体的外接球，所以2R=
考查方向
解题思路
借助长方体作出几何体的三视图如图所示，几何体的外接球，就是正方体的外接球，可直接算出球的表面积。
易错点
容易将几何体的三视图画错。
知识点
6.已知某四棱锥的三视图如图所示，则该四棱锥的侧面积是
A
B
C
D
正确答案
解析
由三视图得四棱锥如下图所示，
故选B。
考查方向
解题思路
由三视图得到几何体为一个四棱锥。根据直观图计算各个侧面面积，即可。
易错点
本题在把几何体的还原成平面直观图上易出错。
知识点
扫码查看完整答案与解析