- 空间几何体的三视图、表面积和体积
- 共1381题
如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且

(1)求证:CD⊥平面PAB;
(2)求点D到平面PBC的距离。
正确答案
见解析。
解析
:(1)∵AB为圆O的直径,∴AC⊥CB,
∵Rt△ABC中,由


∵AB=4,3AD=DB,∴DB=3,
由余弦定理,得△BCD中,CD2=DB2+BC2﹣2DB•BCcos30°=3,
∴CD2+DB2=12=BC2,可得CD⊥AO,
∵点P在圆O所在平面上的正投影为点D,即PD⊥平面ABC,
又∵CD⊂平面ABC,∴PD⊥CD,
∵PD∩AO=D得,∴CD⊥平面PAB,
(2)由(1)可知,PD=DB=3,且Rt△BCD中,
∴
又∵


∴△PBC为等腰三角形,可得
设点D到平面PBC的距离为d,由VP﹣BDC=VD﹣PBC,得


知识点
如图,多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AB=CD=1,
(1)求证;AC⊥CE;
(2)在线段CE上找一点F,使得BF∥平面ACD,并给予证明;
(3)求三棱锥VG﹣BCE的体积。
正确答案
见解析
解析
(1)证明:∵DE⊥平面ACD,∴DE⊥AC,

∴CD∩DE=D,∴AC⊥平面CDE。
∴AC⊥CE。
(2)由已知AB⊥平面ACD,DE⊥平面ACD,∴AB∥ED,
设F为线段CE的中点,H是线段CD的中点,
连接FH,则

∴四边形ABFH是平行四边形,∴BF∥AH,
由BF⊄平面ACD内,AH⊂平面ACD,∴BF∥平面ACD;
(3)由ED⊥平面ACD,∴平面ABED⊥平面ACD,
在平面ACD内作CP⊥AD垂足为P,
∵平面ABED∩平面ACD=AD,∴CP⊥平面ABED,CP为三棱锥VC﹣BGE的高。
由
∵



∴
∵
∴三棱锥VG﹣BCE的体积
知识点
已知圆







正确答案
解析
略
知识点
如图,在四棱锥

(1)求证:EF∥平面PAD;
(2)求证:平面PDC⊥平面PAD
(3)求四棱锥
正确答案
见解析。
解析
(1)证明:连结AC,则


且PA

∴EF∥平面PAD
(2)证明:因为平面PAD⊥平面ABCD, 平面PAD∩平面ABCD=AD,
又CD⊥AD,所以,CD⊥平面PAD,
又CD 
(3) 

又由(2)可知CD⊥平面PAD,CD=2,
知识点
如图所示的几何体,是由棱长为2的正方体
(1)试画出该几何体的三视图;(主视图投影面平行平面
(2)若截面

正确答案
见解析
解析
(1) (每画对一个图形得2分)

(2)设原正方体中由顶点

结合题意,可知,



知识点
若某空间几何体的三视图如图所示,则该几何体的体积是
正确答案
解析
略
知识点
已知空间几何体的三视图如图所示,则该几何体的体积是
正确答案
解析
略
知识点
一个长方体被一个平面截去一部分后所剩几何体的正视图和俯视图如图所示,则该几何体的侧视图可以为( )
正确答案
解析
由题意可知,几何体是长方体被截去正面左上部一个角的图形,如图:
因此它的侧视图是
故选B。
知识点
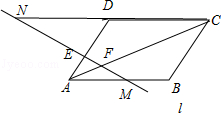
如图,M是平行四边形ABCD的边AB的中点,直线l过点M分别交AD,AC于点E,F,若AD=3AE,则AF:FC= 。
正确答案
1:4
解析
如图所示,设直线l交CD的延长线于点N。
∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD。
∵M是边AB的中点,∴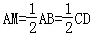
∴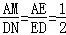
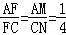
故答案为1:4。
知识点
四棱锥P—ABCD中,底面ABCD是边长为2a的正方形,各侧棱均与底面边长相等,E、F分别是PA、PC的中点。
(1)求证:PC//平面BDE;
(2)求证:平面BDE丄平面BDF;
(3)求四面体E—BDF的体积。
正确答案
见解析。
解析
(1)证明:
连结AC交BD于点O,连结OE
在△PAC中,E、O分别是PA、AC的中点
∴EO//PC


∴PC//平面BDE
(2)证明:∵△PAB是等边三角形且E是PA中点

同理:DE⊥PA
∵PA⊥平面BDE
在△PAC中,F、O分别是PC、AC中点
∴OF//PA

而
∴平面BDE⊥平面BDF
(3)解:

在等边△PAB中,PA=AB=2a,E是PA中点


在等腰△EBD中,EO是底边BD上的高

显然:OF= EO
知识点
扫码查看完整答案与解析