- 空间几何体的三视图、表面积和体积
- 共1381题
11.已知球
A
B
C
D
正确答案
解析
设球O的半径为r，球心O在平面ABC上的射影为M，则M为三角形ABC的外心，由
考查方向
解题思路
先确定M为三角形ABC外接圆的圆心；利用平面几何的知识求出球O的半径，然后带入表面积公式即可。
易错点
不知道球心O在面ABC内的射影的位置；不会构建平面几何的知识求解半径。
知识点
14.已知球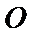
正确答案
解析
求出球的半径为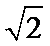
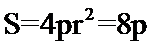
考查方向
解题思路
本题考查空间想象能力，解题步骤如下：先求球的半径再求出其表面积。
易错点
根据已知将球的半径求错。
知识点
11.已知四棱锥
A
B
C
D
正确答案
解析
由题意可得直观图如图所示，
因为
考查方向
解题思路
1)由已知条件画出草图；
2)找到球心的位置，以及构造直角三角形；
3)在直角三角形中计算球的半径，以及表面积.
易错点
本题由题意画出立体几何的图是一个难点，将立体的计算转化为平面也是难点。
知识点
7．如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是
正确答案
知识点
三棱锥S-ABC的所有顶点都在球O的表面上，SA
A
B
C3
D12
正确答案
解析
略
知识点
已知点P，A，B，C，D是球O表面上的点，PA⊥平面ABCD，四边形ABCD是边长为
正确答案
解析
如图所示，∵PA⊥平面ABCD，
∴PA⊥AC。
故可知PC为球O直径，则PC的中点为O，取AC的中点为O′，
则
又∵
∴
∴球半径
∴△OAB为等边三角形。
∴
知识点
若一个球的表面积为
正确答案
1或7
解析
略
知识点
已知空间4个球，它们的半径均为2，每个球都与其他三个球外切，另有一个小球与这4个球都外切，则这个小球的半径为
A
B
C
D
正确答案
解析
由题意可知，小球球心
知识点
3．如图，在一个正方体内放入两个半径不相等的球
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10. 球面上有三点A、B、C，任意两点之间的球面距离都等于球大圆周长的四分之一，且过这三点的截面圆的面积为
A
B
C
D
正确答案
解析
易得OA，OB，OC两两垂直且都为半径R，AB=AC=BC=
考查方向
解题思路
由已知条件先求出球的半径，在求求得体积。
易错点
熟悉等边三角形的性质，以及球面距离与大圆的关系。
知识点
扫码查看完整答案与解析