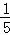- 空间几何体的三视图、表面积和体积
- 共1381题
如图,在三棱柱ABC﹣A1B1C1中,侧面AA1B1B为菱形,且∠A1AB=60°,AC=AB,D是AB的中点。
(1)求证:平面A1DC⊥平面ABC;
(2)求证:BC1∥平面A1DC。
正确答案
见解析。
解析
(1)证明:∵ABB1A1为菱形,且∠A1AB=60°,
∴△A1AB为正三角形,
∵D是AB的中点,∴AB⊥A1D,
∵AC=BC,D是AB的中点,∴AB⊥CD,
∵A1D∩CD=D,∴AB⊥平面A1DC,
∵AB⊂平面ABC,∴平面A1DC⊥平面ABC,
(2)证明:连结C1A,设AC1∩A1C=E,连结DE。
∵三棱柱的侧面AA1C1C是平行四边形,∴E为AC1中点,
在△ABC1中,又∵D是AB的中点,∴DE∥BC1,
∵DE⊂平面A1DC,BC1不包含于平面A1DC,
∴BC1∥平面A1DC,
知识点
已知向量



正确答案
解析
因为向量















知识点
在如图所示的组合体中,三棱柱




(1)求证:无论点


(2)当点


正确答案
见解析
解析
(1)∵侧面




又圆柱母线





又


∵



(2)设圆柱的底面半径为

当点




知识点
在一次珠宝展览会上,某商家展出一套珠宝首饰,第一件首饰是1颗珠宝, 第二件首饰是由6颗珠宝构成如图1所示的正六边形, 第三件首饰是由15颗珠宝构成如图2所示的正六边形, 第四件首饰是由28颗珠宝构成如图3所示的正六边形, 第五件首饰是由45颗珠宝构成如图4所示的正六边形, 以后每件首饰都在前一件上,按照这种规律增加一定数量的珠宝,使它构成更大的正六边形,依此推断第6件首饰上应有__________颗珠宝;则第

正确答案
66;
解析
设珠宝数构成了一个数列{an},则有a1=1,a2=a1+5=6,a3=a2+5+4=15,a4=a3+5+2×4=28,a5=a4+5+3×4=45,a6=a5+5+4×4=66,…,
an=an-1+5+4(n-2),所以an=a1+5(n-1)+4[1+2+3+…+(n-2)]=2n2-n.
知识点
四棱锥P﹣ABCD的底面ABCD是边长为2的正方形,PA⊥底面ABCD且PA=4,则PC与底面ABCD所成角的正切值为 。
正确答案
解析
连接AC,则
∵PA⊥底面ABCD,
∴∠PCA是PC与底面ABCD所成角,
∵四棱锥P﹣ABCD的底面ABCD是边长为2的正方形,
∴AC=2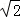
∵PA=4,
∴tan∠PCA=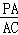
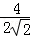
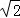
知识点
已知单位向量


正确答案
1
解析
∵单位向量






知识点
如图,棱柱



(1)求证:平面

(2)设






正确答案
见解析
解析
(1)证明:


故



(2)记















因为底面
则



故


知识点
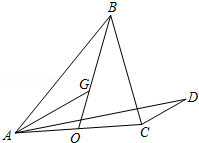
如图,在△ABC中,BO为边AC上的中线,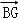
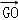
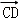
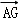
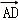
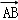
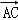
正确答案
解析
由已知得G是三角形的重心,因此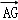
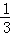
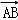
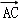
由于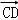
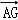
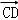
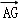
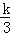
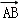
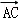
那么可得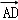
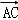
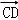
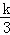
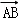
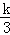
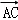
∵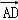
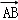
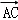
∴k=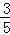
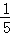
知识点
已知




正确答案
解析
由题意,

知识点
已知某几何体的三视图如下,则该几何体体积为 。
正确答案
解析
该几何体是一个圆柱与一个长方体的组成,其中重叠了一部分

知识点
扫码查看完整答案与解析