- 空间几何体的三视图、表面积和体积
- 共1381题
如图,已知AC⊥平面CDE,BD//AC,△ECD为等边三角形,F为ED边的中点,CD=BD=2AC=2
(1)求证:CF∥面ABE;
(2)求证:面ABE⊥平面BDE:
(3)求三棱锥F—ABE的体积。
正确答案
见解析
解析
(1)证明:取BE的中点G,连FG∥


(2)证明:△ECD为等边三角形,得到CF⊥ED又CF⊥BD
而CF∥AG ,故

(3)由CF⊥面BDE,

知识点
直线y=

正确答案
解析
如图,

由圆的性质可知

故
知识点
如图,在四棱锥









(1)求证:MQ//平面
(2)若


正确答案
见解析
解析
(1)取



因为



又因为


因为四边形
所以

所以四边形
所以MQ//BE,因为



所以MQ//平面
(2)因为



所以






所以



所以
又





所以




又


又






又

知识点
已知向量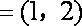
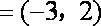
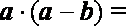
正确答案
4
解析
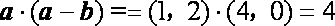
知识点
某圆锥的侧面展开图是半径为1cm的半圆,则该圆锥的体积是 ▲ cm
正确答案
解析
设圆锥的底面圆的半径为




体积
知识点
设





(1)求边
(2)求
正确答案
见解析
解析
(1)由
因为

所以
所以
(2)因为

所以
所以
因为



所以
知识点
已知一四棱锥P-ABCD的三视图如下,E是侧棱PC上的动点。

(1)求四棱锥P-ABCD的体积;
(2)是否不论点E在何位置,都有BD⊥AE?证明你的结论;
(3)求四棱锥P-ABCD的侧面积.
正确答案
见解析。
解析
(1)解:由该四棱锥的三视图可知,该四棱锥P-ABCD的底面是
侧棱PC⊥底面ABCD

(2) 不论点E在何位置,都有BD⊥AE。证明如下:连结AC,∵ABCD是正方形
∴BD⊥AC ∵PC⊥底面ABCD 且

又∵

∴不论点E在何位置,都有BD⊥AE
(3) 由(1)知PC⊥CD,PC⊥BC,CD=CB, ∴Rt△PCD≌Rt△PCB
∵AB⊥BC,AB⊥PC, 

同理AD⊥PD,∴四棱锥P-ABCD的侧面积


知识点
如图甲,一个正方体魔方由27个单位(长度为1个单位长度)小立方体组成,把魔方中间的一层



(1)试用

(2)求魔方增加的表面积的最大值。
正确答案
见解析。
解析
(1)由题意得
解得
(2)魔方增加的表面积为
由(1)得
令
则


答:当

知识点
已知三棱锥P﹣ABC的所有棱长都相等,现沿PA,PB,PC三条侧棱剪开,将其表面展开成一个平面图形,若这个平面图形外接圆的半径为
正确答案
9
解析
解:根据题意几何体为正三棱锥,如图,
PD=



设棱长为a,则OD+PD=





V棱锥=


知识点
如图,AB,CD均为圆O的直径,CE⊥圆O所在的平面,BF∥CE,求证:
(1)平面BCEF⊥平面ACE;
(2)直线DF∥平面ACE。
正确答案
见解析
解析
证明:(1)因为CE⊥圆O所在的平面,BC⊂圆O所在的平面,
所以CE⊥BC,
因为AB为圆O的直径,点C在圆O上,所以AC⊥BC,
因为AC∩CE=C,AC,CE⊂平面ACE,
所以BC⊥平面ACE,
因为BC⊂平面BCEF,所以平面BCEF⊥平面ACE,
(2)由(1)AC⊥BC,又因为CD为圆O的直径,
所以BD⊥BC,
因为AC,BC,BD在同一平面内,所以AC∥BD,
因为BD⊄平面ACE,AC⊂平面ACE,所以BD∥平面ACE,
因为BF∥CE,同理可证BF∥平面ACE,
因为BD∩BF=B,BD,BF⊂平面BDF,
所以平面BDF∥平面ACE,
因为DF⊂平面BDF,所以DF∥平面ACE
知识点
扫码查看完整答案与解析