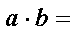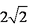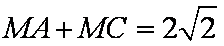- 空间几何体的三视图、表面积和体积
- 共1381题
已知向量
(1)求
(2)若
正确答案
(1)
(2)由
解析
考查向量的数量积运算、向量求摸、换元转换求函数值域问题以及导数在研究函数值域方面的运用;(2)考查向量的遇模平方以及等量转换,函数与方程的思想和解不等式组;整个试题综合性较高,考查的知识较多,运算量较大是一个中等偏上的试题。
知识点
在平面直角坐标系xOy中,已知向量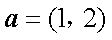
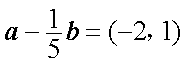
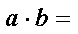
正确答案
25
解析
由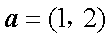
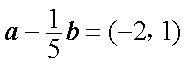
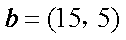
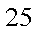
知识点
如图所示,已知ΔBCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,该几何体的侧视图(左视图)的面积为


(1)求AB的长;
(2)求证:对任意的
(3)当
正确答案
见解析
解析
(1)

取BD的中点为M,连接CM,则CM⊥BD,且





(2) 


(3)


由(2)EF∥CD,∴EF⊥平面ABC,∵BE
又∵EF,AC

从而平面BEF⊥平面ACD,在
当BE⊥AC时,
故当
知识点
已知正方形
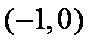
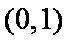
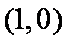
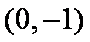
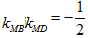
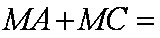
正确答案
解析
设点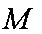
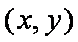
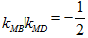
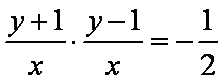
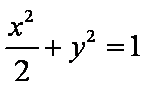
知识点
已知一个几何体的三视图如下,正视图和俯视图两个等腰梯形,长度单位是厘米,那么该几何体的体积是( )
正确答案
解析
由图可知,该几何体是上下底面是正方形,高度是3的四棱台,
根据台体的体积公式


知识点
已知E、F分别是正方体

角的正弦值是( )
正确答案
解析
解析 :设正方体





角的正弦值是
知识点
在平面直角坐标系xOy中,过原点O的直线与函数

正确答案
解析
设

则

因为BC//x轴,所以
即
又A、B、O三点共线,故
由①②得
故四边形ABCD的面积为
知识点
在直三棱柱



(1)求证:直线

(2)求证:平面

正确答案
见解析
解析
(1)证明:由直三棱柱
而

(2)因为三棱柱


而


所以
又

知识点
如图所示,在棱长为2的正方体




(1)求证:

(2)求证:
(3)求三棱锥
正确答案
见解析。
解析
(1)
连结





(2)
(3)


∴
即

=
知识点
已知平面向量





正确答案
解析
如图所示:
知识点
扫码查看完整答案与解析