- 空间几何体的三视图、表面积和体积
- 共1381题
如图,在长方体



(1)求证:

(2)求证:平面

(3)求四面体
正确答案
见解析
解析
(1)证明:连


则





(2) 由已知得

由长方体的特征可知:









(3)四面体D1B1AC的体积

知识点
已知某几何体的三视图如图所示,则该几何体的体积为 。
正确答案
解析
解:由已知中的三视图可得几何体是一个三棱锥
且棱锥的底面是一个以(2+1)=3为底,以1为高的三角形
棱锥的高为3
故棱锥的体积V=

故答案为:
知识点



正确答案
解析
∵











知识点
已知某几何体的三视图如图所示,则该几何体的体积为 。
正确答案
解析
由已知中的三视图可得几何体是一个三棱锥
且棱锥的底面是一个以(2+1)=3为底,以1为高的三角形
棱锥的高为3
故棱锥的体积V=

知识点
如图,在三棱柱ABC-A1B1C1中,
(1)若BB1=BC,B1C⊥A1B,证明:平面AB1C
(2)设D是BC的中点,E是A1C1上的一点,且A1B∥平面
正确答案
解析
(1)因为BB1=BC,所以侧面BCC1B1是菱形,所以B1C⊥BC1,
又因为B1C⊥A1B ,且A1B∩BC1=B,所以BC1⊥平面A1BC1,
又B1C
(2)设B1D交BC1于点F,连结EF,则平面A1BC1∩平面B1DE=EF。
因为A1B//平面B1DE, A1B
所以

又因为



知识点
如图,是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是 。
正确答案
解析
由三视图知,几何体是半个圆锥,
圆锥的底面半径是1,母线长是2,
∴圆锥的高是
∴圆锥的体积是
知识点
如图,三棱柱ABC﹣A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(1)证明:平面BDC1⊥平面BDC
(2)平面BDC1分此棱柱为两部分,求这两部分体积的比。
正确答案
见解析。
解析
(1)由题设知BC⊥CC1,BC⊥AC,CC1∩AC=C,
∴BC⊥平面ACC1A1,又DC1⊂平面ACC1A1,
∴DC1⊥BC。
由题设知∠A1DC1=∠ADC=45°,
∴∠CDC1=90°,即DC1⊥DC,又DC∩BC=C,
∴DC1⊥平面BDC,又DC1⊂平面BDC1,
∴平面BDC1⊥平面BDC;
(2)设棱锥B﹣DACC1的体积为V1,AC=1,由题意得V1=


又三棱柱ABC﹣A1B1C1的体积V=1,
∴(V﹣V1):V1=1:1,
∴平面BDC1分此棱柱两部分体积的比为1:1
知识点
在如图所示的四棱锥




(1)求异面直线

(2)求证:平面

(3)求直线

正确答案
见解析。
解析
(1)∵
∴异面直线



所以


∵
∴
又



由已知可求得
∴在
即异面直线

(2)∵

∴

又
∴
∵
∴
又
所以平面
(3)
取



由(Ⅱ)知
则
所以






∴
即直线

知识点
已知正四棱柱ABCD﹣A1B1C1D1中,AA1=2AB,E为AA1中点,则异面直线BE与CD1所成角的余弦值为( )
正确答案
解析
如图连接A1B,则有A1B∥CD1,
∠A1BE就是异面直线BE与CD1所成角,
设AB=1,
则A1E=AE=1,∴BE=

由余弦定理可知:cos∠A1BE=
故选C。
知识点
已知某几何体的三视图如图所示,根据图中标出的尺寸(单位cm),可得这个几何体的体积是 cm3。
正确答案
12
解析
由三视图可知:该几何体可以看成一个棱长为4,2,3的长方体的一半。
∴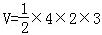
故答案为12。
知识点
扫码查看完整答案与解析