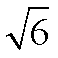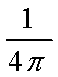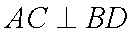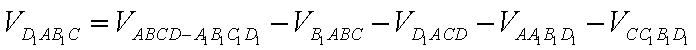- 空间几何体的三视图、表面积和体积
- 共1381题
已知复数z满足
正确答案
解析
略
知识点
如图, 已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且
求证:(1)EC⊥CD ;
(2)求证:AG∥平面BDE;
(3)求:几何体EG-ABCD的体积。
正确答案
见解析
解析
(1)证明:由平面ABCD⊥平面BCEG,
平面ABCD∩平面BCEG=BC, 

又CD
(2)证明:在平面BCDG中,过G作GN⊥CE交BE于M,连
DM,则由已知知;MG=MN,MN∥BC∥DA,且



∵DM


(3)解:

知识点
己知向量a,b满足|a|= 2,|b|=1, (6-2a)丄b,则|a+b|=
正确答案
解析
由题意可知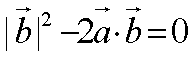
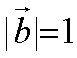
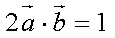
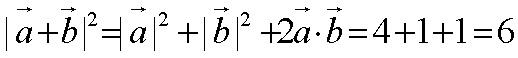
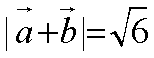
知识点
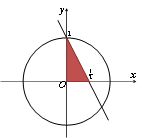
向平面区域{(x,y)|x2+y2≤1}内随机投入一点,则该点落在区域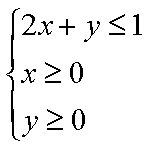
正确答案
解析
如图所示:落在阴影部分内的概率为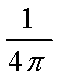
知识点
下列四个图中,函数
正确答案
解析
略
知识点
某圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为
正确答案
2π
解析
略
知识点
设

正确答案
1+
解析
略
知识点
如图,平面

(1)当点E为AD的中点时,求证:EF//平面PBD;
(2)求证:无论点E在线段AD的何处,总有
正确答案
见解析
解析
(1)证明: 在三角形

所以

在


所以
又
所以

(2)因为平面





所以

又





所以
又
所以无论点


知识点
如图,过圆E外一点A作一条直线与圆E交B,C两点,且AB=

(1)求AF的长。
(2)求证:AD=3ED。
正确答案
见解析。
解析
(1) 延长




又


又

所以根据切割线定理

(2) 过




从而有

知识点
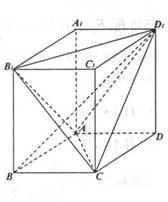
如图,直四棱柱ABCD-A1B1C1D1底面ABCD为菱形,AB=1 AA1= 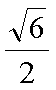
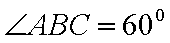
(1)求证:AC丄BD1
(2)求四面体D1AB1C的体积
正确答案
见解析。
解析
(1) 连结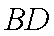
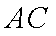
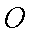
因为四边形
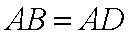

则
由直四棱柱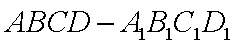
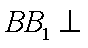

可知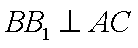
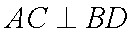
则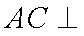
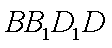
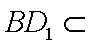
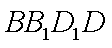
则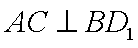
(2)
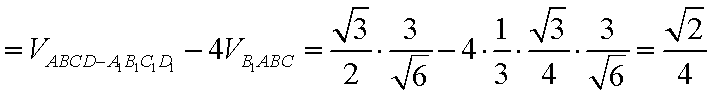
知识点
扫码查看完整答案与解析