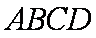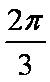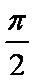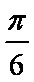- 空间几何体的三视图、表面积和体积
- 共1381题
如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB=

(1)求证:BC⊥AF;
(2)试判断直线DF与平面BCE的位置关系,并证明你的结论。
正确答案
见解析。
解析
(1)证明:取AB中点H,连结CH,
∵底面ABCD是梯形,且AD=DC=CB=
∴CD=AH,CD∥AH,
∴四边形AHCD为平行四边形,
∴AD=HC=
∴∠ACB=90°,
∴BC⊥AC,
∵平面ACEF⊥平面ABCD,且平面ACEF∩平面ABCD=AC,
∴BC⊥平面ACEF,
而AF⊂平面ACEF,
故BC⊥AF,
(2)DF∥平面BCE,以下证明:
取AC的中点M,连接DM,FM。
∵在平面ABCD中,DM⊥AC,BC⊥AC,
∴DM∥BC,
∵在直角梯形ACEF中,
∴FM∥EC,
∵BC,CE⊂平面BCE,BC∩CE=C,DM,MF⊂平面DMF,DM∩MF=M,
∴平面BCE∥平面DMF,DF⊂平面DMF,
∴DF∥平面BCE。
知识点
如图,四棱锥P-ABCD中,底面ABCD是边长为1的正方形,CD⊥平面PAD,PA⊥AD,PA=2,E分别PC的中点,点P在棱PA上。
(1)求证:AC⊥DE;
(2)求三棱锥E-BDF的体积。
正确答案
见解析
解析
(1)连接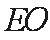
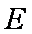
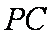
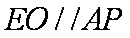
因为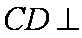
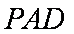
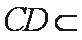
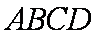
所以平面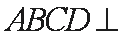
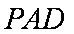
且平面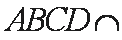
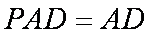

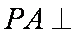
所以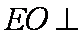
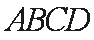
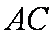
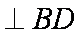

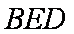
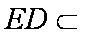
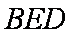
所以
(2)由(1)知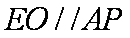
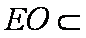
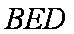
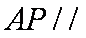
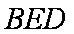
又
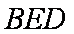
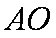
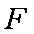
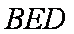
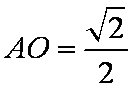
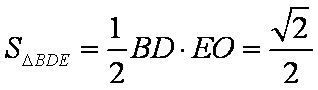
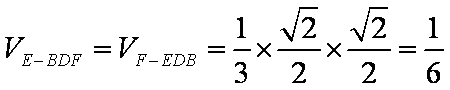
解法二
(2)由(1)知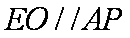
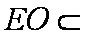
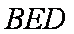
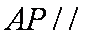
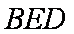
所以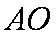
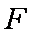
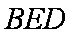

知识点
一个几何体的三视图如图所示,则该几何体的体积是( )
正确答案
解析
由三视图知为几何体为四棱柱,且四棱柱的高为2,底面为等腰梯形,等腰梯形的两底边长分别为2,2+1+1=4,高为2,
∴四棱柱的体积V=
知识点
如图所示,






(1)证明:
(2)求

(3)求三棱锥
正确答案
见解析。
解析
(1)证明:取

∵△BCE正三角形,∴EF

,又AD⊥平面ABC∴AD∥EF,∴
∴


故
(2)由(1)知B在平面

故


在Rt△ABD中,BD2=AB2+AD2,求得BD=4,
在Rt△BDF中,sin∠BDF =
(3)由(1)知EF∥AD 所以有
所以
即
方法不唯一,只要过程,结论正确给分。
知识点
已知△ABC的三个顶点都在抛物线y2=2px(p>0)上,且抛物线的焦点F满足
(1)求p的值;
(2)O为抛物线的顶点,△OFA、△OFB、△OFC的面积分别记为S1、S2、S3,求证:
正确答案
见解析。
解析
(1)∵抛物线的焦点F满足
∴
取BC边上的中点M,则AF=2FM,
故点F在直线l上,
令y=0,得x=1,得抛物线的焦点F(1,0),
于是,
(2)证明:记A(x1,y1),B(x2,y2),C(x3,y3),
由

于是,


知识点
设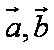
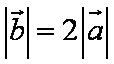
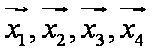
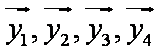
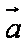
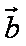
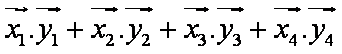
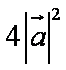
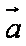
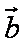
正确答案
解析
略
知识点
空间几何体的外接球,理解为琼将几何体包围,几何体的顶点和弧面在此球上
正确答案
解析
略
知识点
如图,已知三棱锥







(1)求证:

(2)求证:平面

(3)若


正确答案
见解析。
解析
(1)∵M为AB中点,D为PB中点,
∴MD//AP, 又∴MD
∴DM//平面APC。 …………………………………………………3分
(2)∵△PMB为正三角形,且D为PB中点,∴MD⊥PB。
又由(1)∴知MD//AP, ∴AP⊥PB。
又已知AP⊥PC ∴AP⊥平面PBC,
∴AP⊥BC, 又∵AC⊥BC。 ………………………………………7分
∴BC⊥平面APC, ∴平面ABC⊥平面PAC,
(3)∵ AB=20
∴ MB=10 ∴PB=10
又 BC=4,
∴
又MD
∴VD-BCM = VM-BCD =
知识点
如图所示是一个几何体的三视图,其侧视图是一个边长为a的等边三角形,俯视图是两个正三角形拼成的 菱形,则该几何体的体积为
正确答案
解析

知识点
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D。现测得∠BCD=


正确答案
解析
在

由正弦定理得
所以
在

知识点
扫码查看完整答案与解析