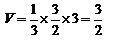空间几何体的三视图、表面积和体积
共1381题

空间几何体的三视图、表面积和体积
共1381题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

19.如图，在长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，M为棱DD1上的一点。

（1）求三棱锥A-MCC1的体积；

（2）当A1M+MC取得最小值时，求证：B1M⊥平面MAC

正确答案

见解析。

解析

（1）又长方体AD平面.点A到平面的距离AD=1，

∴==×2×1=1 ，∴

（2）将侧面绕逆时针转动90°展开，与侧面共面。当，M，C共线时，

+MC取得最小值AD=CD=1 ，=2得M为的中点连接M在中，=MC=，=2，

∴=+ ， ∴∠=90°，CM⊥，

∵⊥平面，∴⊥CM ∵AM∩MC=C

∴CM⊥平面，同理可证⊥AM ∴⊥平面MAC

知识点

空间几何体的结构特征

题型：简答题

简答题 · 12 分

21.设F1，F2分别是C：+=1（a＞b＞0）的左，右焦点，M是C上一点且MF2与x轴垂直，直线MF1与C的另一个交点为N。

（1）若直线MN的斜率为，求C的离心率；

（2）若直线MN在y轴上的截距为2，且|MN|=5|F1N|，求a，b。

正确答案

见解析。

解析

（1）∵M是C上一点且MF2与x轴垂直，∴M的横坐标为c，当x=c时，y=，即M（c，），

若直线MN的斜率为，即tan∠MF1F2=，即b2==a2﹣c2，即c2﹣﹣a2=0，

则，解得e=。

（2）由题意，原点O是F1F2的中点，则直线MF1与y轴的交点D（0，2）是线段MF1的中点，故=4，即b2=4a，

由|MN|=5|F1N|，解得|DF1|=2|F1N|，设N（x1，y1），由题意知y1＜0，

则，即代入椭圆方程得，

将b2=4a代入得，解得a=7，b=

知识点

空间几何体的结构特征

题型：简答题

简答题 · 12 分

19.如图所示，矩形中，，。，分别在线段和上，∥，将矩形沿折起，记折起后的矩形为，且平面平面。

（Ⅰ）求证：∥平面；

（Ⅱ）若，求证：；

（Ⅲ）求四面体体积的最大值，

正确答案

见解析。

解析

（Ⅰ）证明：因为四边形，都是矩形，所以 ∥∥，。

所以四边形是平行四边形，

所以 ∥，

因为平面，所以 ∥平面，

（Ⅱ）证明：连接，设。

因为平面平面，且，所以平面

所以，

又，所以四边形为正方形，所以，

所以平面，所以，

（Ⅲ）解：设，则，其中，由（Ⅰ）得平面，

所以四面体的体积为，

所以，

当且仅当，即时，四面体的体积最大。

知识点

空间几何体的结构特征

题型：填空题

填空题 · 5 分

15.如图放置的正方形，,、分别在轴、轴的正半轴（含原点）上滑动，则的最大值为_________________

正确答案

解析

解：如图令∠OAD=θ，由于AD=1故0A=cosθ，OD=sinθ，
如图∠BAX= ，AB=1，做垂直于x轴于故，故（cosθ+sinθ，cosθ）
同理可求得=（sinθ，cosθ+sinθ），
∴cosθ+sinθ，cosθ）•（sinθ，cosθ+sinθ）=1+sin2θ，

的最大值是2，故答案是 2

知识点

空间几何体的结构特征

题型：单选题

单选题 · 5 分

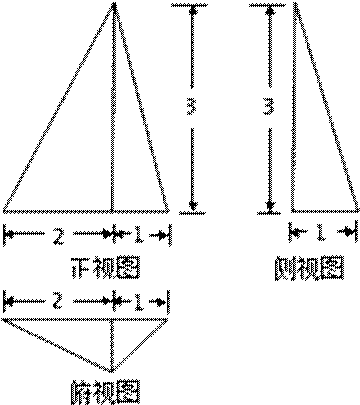
9.已知某几何体的三视图如上图所示，则该几何体的体积为 ( )

正确答案

解析

由三视图易知，该几何体是底面积为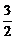，高为3的三棱锥，由锥体的体积公式得

知识点

空间几何体的结构特征

题型：单选题

单选题 · 5 分

如图，P（x0 , f (x0））是函数y =f (x)图像上一点，曲线y =f (x)在点P处的切线交x轴于点A，PB⊥x轴，垂足为B. 若ΔPAB的面积为，则与满足关系式

正确答案

解析

易知：切线方程为，令，又，所以，，所以，即。

知识点

空间几何体的结构特征

题型：单选题

单选题 · 5 分

如图是一个几何体的三视图，则该几何体的体积是

正确答案

解析

知识点

空间几何体的结构特征

题型：单选题

单选题 · 5 分

6.已知向量a=（x-1，2），b=（2，1），则a⊥b的充要条件是（）

Ax=-

Bx=-1

Cx=5

Dx=0

正确答案

解析

有向量垂直的充要条件得2（x-1）+2=0 所以x=0 ，选D。

知识点

空间几何体的结构特征

题型：单选题

单选题 · 5 分

3.一个几何体的三视图形状都相同，大小均等，那么这个几何体不可以是（）

A球

B三棱锥

C正方体

D圆柱

正确答案

解析

分别比较A、B、C的三视图不符合条件，D 符合。

知识点

空间几何体的结构特征

题型：填空题

填空题 · 5 分

16.在等腰梯形中，，，是的中点，将与分别沿边、向上折起，使、重合于点,则三棱锥的外接球的表面积为___________

正确答案

解析

解：设DC的中点为F，PE的中点为H，连接FH由折叠的三棱人锥可知球心O在FH上，，设OF=x,FC=2,AH=2，，FH=所以所以，，可得，那么可求出球的表面积

知识点

空间几何体的结构特征

继续学习学习下一知识点

下一知识点 : 空间点、线、面的位置关系

百度题库 > 高考 > 文科数学 > 空间几何体的三视图、表面积和体积

扫码查看完整答案与解析