- 空间几何体的三视图、表面积和体积
- 共1381题
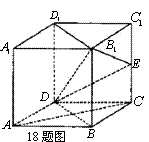
14.正四面体
正确答案
解析
将四面体ABCD放置于正方体中，如图所示
可得正方体的外接球就是四面体ABCD的外接球，
∵正四面体ABCD的棱长为4，
∴正方体的棱长为
可得外接球半径R满足2R＝
E为棱BC的中点，过E作其外接球的截面，当截面到球心O的距离最大时，
截面圆的面积达最小值，
此时球心O到截面的距离等于正方体棱长的一半，
可得截面圆的半径为r=
得到截面圆的面积最小值为S=
故答案为：4π
知识点
5.已知某几何体的三视图（单位：cm）如图所示，则该几何体的体积是( )
A
B100
C92
D84
正确答案
解析
如图所示，原几何体为：
一个长宽高分别为6，3，6的长方体砍去一个三棱锥，底面为直角边分别为3，4直角三角形，高为4．因此该几何体的体积=3×6×6﹣
知识点
5.已知圆锥的母线长为
正确答案
解析
知识点
19.在长方体
(1) 求几何体
(2)求异面直线
正确答案
见解析。
解析
(1)
左视图如下图所示．
(2)依据题意，有
∴
又
∴
∴异面直线
知识点
13.已知直线
正确答案
±2
解析
因为向量
【思路点拨】本题先由向量加法与减法的几何意义得到OA⊥OB，再由所给直线与圆的特殊性确定实数a的值.
知识点
18.如图，已知四棱柱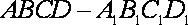
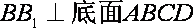
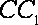
（1）求证：
（2）求证：AC∥平面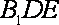
正确答案
见解析。
解析
（1）因为底面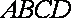
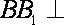
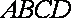
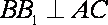
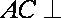
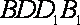
（2）设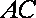
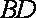
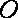
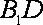
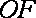
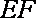
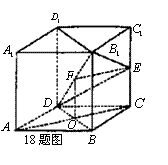
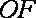
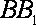
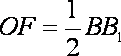
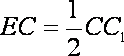
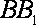
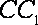
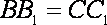
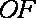
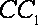
且
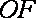
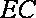
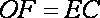
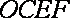
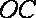
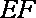
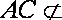
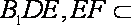
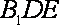
所以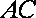
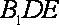
知识点
10.某同学为了研究函数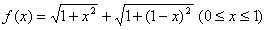
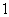
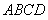
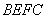
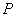
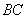
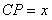
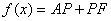
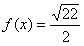
正确答案
解析
从图中知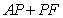
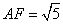
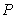
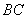
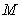
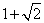
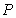
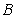
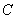
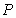
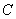
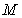
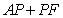
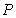
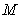
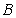
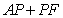
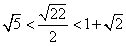
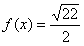
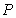
知识点
13.已知
正确答案
解析
∵
∴
知识点
4.执行如图所示程序框图所表达的算法，若输出的x值为48，则输入的x值为（ ）
正确答案
解析
x←2x，n=1+1=2，满足n≤3，执行循环体；
x=2×（2x）=4x，n=2+1=3，满足n≤3，执行循环体；
x=2×（4x）=8x，n=3+1=4，不满足n≤3，退出循环体，
由8x=48即可得x=6．
则输入的x值为：6．
故选B.
知识点
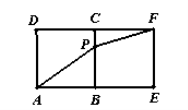
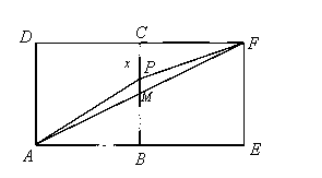
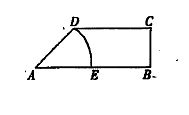
6.一只受伤的丹顶鹤在如图所示（直角梯形）的草原上飞过其中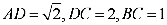
A
B
C
D
正确答案
解析
过点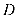
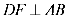
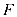
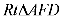
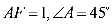
梯形的面积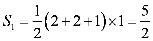
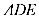
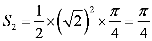
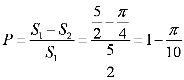
知识点
扫码查看完整答案与解析