空间几何体的三视图、表面积和体积
共1381题

空间几何体的三视图、表面积和体积
共1381题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

14．某几何体的三视图如图所示，则该几何体的表面积为__________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

简答题 · 12 分

18.如图，ABCD是边长为2的正方形，平面ABCD，平面ABCD，DE=2AF，BE与平面ABCD所成角为45°．

（Ⅰ）求证：平面BDF；

（Ⅱ）求证：AC//平面BEF；

（Ⅲ）求几何体EFABCD的体积．

正确答案

解：

（I）证明：∵平面ABCD，平面ABCD，∴．

∵ABCD是正方形，∴，∴平面BDE．

（II）证明：延长DA，EF相交于点M，连接BM，

∵平面ABCD，平面ABCD，∴AF//DE，

又DE=2AF，∴AM=AD=2，

∵AD BC，∴AM BC，四边形AMBC为平行四边形，

∴AC//MB，

又MB 平面BEF，AC平面BEF，

∴AC//平面BEF．

（III）由（II）可知几何体EFABCD的体积等于四棱锥的体积减去四棱锥的体积．

∵，四边形MBCD为直角梯形，

平面ABCD，平面ABCD，DE=2AF，AF=，DE=，

所以几何体EFABCD的体积为

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

单选题 · 5 分

5．如图，网格纸上小正方形边长为1，粗线是一个棱锥的三视图，则此棱锥的表面积为（）

正确答案

解析

直观图如图所示四棱锥，，

，，

故此棱锥的表面积为，故选A.

知识点

空间几何体的结构特征

题型：简答题

简答题 · 12 分

20．已知椭圆的中心在坐标原点，右焦点为，、是椭圆的左、右顶点，是椭圆上异于、的动点，且面积的最大值为．

（1）求椭圆的方程；

（2）是否存在一定点（），使得当过点的直线与曲线相交于，两点时，为定值？若存在，求出定点和定值；若不存在，请说明理由.

正确答案

解：

（1）设椭圆的方程为（），由已知可得①，∵为椭圆右焦点，∴②，

由①②可得，，

椭圆的方程为；

（2）过点取两条分别垂直于轴和轴的弦，，

则，即，

解得，∴若存在必为，定值为3，

下证满足题意，

设过点的直线方程为，代入中得：，设，，则，，

，综上得定点为，定值为3.

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

简答题 · 12 分

19．在四棱锥中，平面，底面为直角梯形，∥，，,。

（Ⅰ）求异面直线与所成角的大小；

（Ⅱ）求直线与平面所成角的正弦值。

正确答案

解一：（Ⅰ）直角梯形中∥异面直线所成的角就是所成的角（或其补角）。连结

由已知有

所以是等腰直角三角形，所以

故异面直线与所成角为

（Ⅱ）由已知有

直角梯形中

设到平面的距离为，由

由（Ⅰ）知；设与平面所成角为，则有

解法二：以为原点，为轴建立坐标系

（Ⅰ）

（Ⅱ）可求得平面的一个法向量为，设与平面所成角为，

有

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

简答题 · 13 分

20．在xoy平面上有一点列，点位于曲线（）上，以点为圆心的⊙与X轴都相切，且⊙与⊙又彼此外切，若，且（）。

（1）求证：数列是等差数列；

（2）设⊙的面积为，，求。

正确答案

解：（1）∵以点为圆心的⊙与X轴都相切，

∴⊙的半径

又∵⊙与⊙彼此外切，∴|⊙⊙|

∴

即

∵，∴

∴是以为首项，公差为2的等差数列。

（2）由（1）得

又

∴

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

简答题 · 13 分

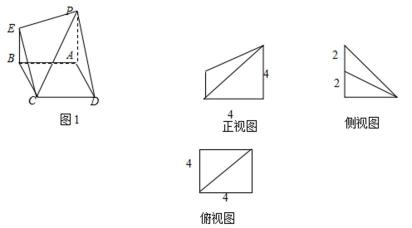
18.图1是一几何体的直观图，右图是该几何体的三视图。

（I）若F为PD的中点，求证AF⊥平面PCD；

（II）求几何体BCE—APD的体积；

（III）若PB和AE交于G点，求四棱锥G—ABCD的体积。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

单选题 · 5 分

5．一组数据3，4，5，s，t的平均数是4，中位数是m，则过点和的直线与直线的位置关系是（）

A平行

B相交但不垂直

C重合

D垂直

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

单选题 · 5 分

9.给定两个模为1的平面向量和，它们的夹角为，如图，点C在以O为圆心的圆弧AB上运动，若，其中，则的最大值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

单选题 · 5 分

3．设与垂直，则的值等于（）

D-l

正确答案

解析

由题意得：所以因此选B.

知识点

空间几何体的结构特征

继续学习学习下一知识点

下一知识点 : 空间点、线、面的位置关系

百度题库 > 高考 > 文科数学 > 空间几何体的三视图、表面积和体积

扫码查看完整答案与解析