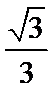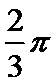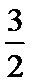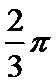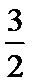- 空间几何体的三视图、表面积和体积
- 共1381题
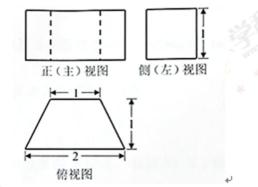
11.某四棱柱的三视图如图所示，则该四棱柱的体积为___________.
正确答案
3/2
知识点
11. 某几何体的三视图如图所示（单位：cm），则该几何体的表面积是_____cm2，体积是_____cm3.
正确答案
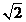
知识点
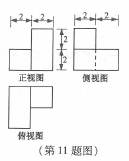
3.将一个长方形沿相邻三个面的对角线截去一个棱锥，得到的几何体的正视图与俯视图如图所示，则该几何体的侧（左）视图为
A
B
C
D
正确答案
知识点
如图,长方体
21.在图中画出这个正方形（不必说明画法与理由）；
22.求平面
正确答案
解析
试题分析：分别在
交线围成的正方形
考查方向
解题思路
立体几何解答题在高考中难度低于解析几何,属于得分题,往年第一问多为线面位置关系的证明,今年试题有所创新，改为作截面图.
易错点
截面位置的确定
正确答案
解析
试题分析：长方体被平面
作
考查方向
解题思路
立体几何解答题在高考中难度低于解析几何,属于得分题,往年第一问多为线面位置关系的证明,今年试题有所创新，改为作截面图,令人耳目一新.第二问求两几何体体积之比,方法容易想到,注意运算不要出现错误.
易错点
注意运算正确性
5.一个由半球和四棱锥组成的几何体，其三视图如图所示.则该几何体的体积为
A
B
C
D
正确答案
知识点
12.已知某三菱锥的三视图如图所示，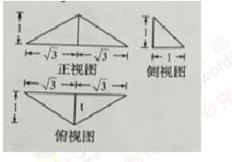
正确答案
解析
由三视图可知该几何体是一个三棱锥，且底面积为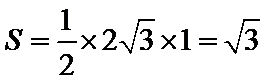
考查方向
解题思路
本题考查三视图，考查几何体体积，考查学生的识图能力．解题时要求我们根据三视图想象出几何体的形状，由三视图得出几何体的尺寸，为此我们必须掌握基本几何体（柱、锥、台、球）的三视图以及各种组合体的三视图．
易错点
本题易在观察三视图的量的时候出错。
知识点
7．某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为（ ）
A
B
C
D
正确答案
解析
四棱锥的直观图如图所示：
由三视图可知，
考查方向
解题思路
几何体是四棱锥，且四棱锥的一条侧棱与底面垂直，结合直观图求相关几何量的数据，可得答案.
易错点
几何体框空间结构的判断
知识点
5.一个几何体的三视图如图所示，则该几何体的表面积为（ ）
A
B
C
D
正确答案
解析
由几何体的三视图可知该几何体为圆柱的截去一半，所以该几何体的表面积为
考查方向
解题思路
解题时要看清楚是求表面积还是求体积，否则很容易出现错误．本题先根据三视图判断几何体的结构特征，再计算出几何体各个面的面积即可．
易错点
所给几何体空间结构的判断
知识点
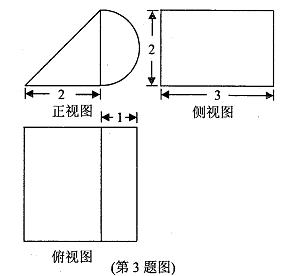
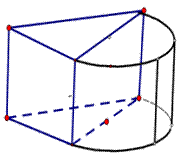
3．某几何体的三视图如图所示(单位：cm)，则该几何体的体积等于（ ）cm3
A4+
B4+
C6+
D6+
正确答案
解析
将三视图画出直方图然后在旋转为立体图形。为三棱柱和半个圆柱。体积为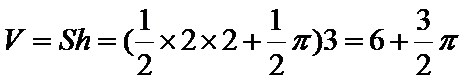
考查方向
解题思路
将三视图画出直方图然后在旋转为立体图形。
易错点
看成三棱锥，而出现错误。
知识点
11. 在封闭的直三棱柱
A4π
B
C6π
D
正确答案
解析
要使球的体积V最大，必须球的半径R最大，由题意知球的与直三棱柱的上下底面都相切时，球的半径的取得最大值
考查方向
解题思路
要使球的体积V最大，必须球的半径R最大，由题意知球的与直三棱柱的上下底面都相切时，球的半径的取得最大值
易错点
对三棱柱的内切球和球的体积理解出现错误、计算错误
知识点
扫码查看完整答案与解析