抛物线的标准方程和几何性质
共169题

· 抛物线的标准方程和几何性质

抛物线的标准方程和几何性质
共169题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：单选题

单选题 · 5 分

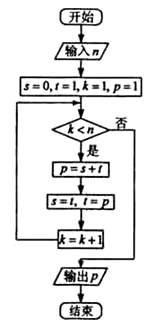
执行右面的程序框图，如果输入的n是4，则输出的P是

正确答案

解析

略

知识点

抛物线的标准方程和几何性质

题型：单选题

单选题 · 5 分

设M(，)为抛物线C：上一点，F为抛物线C的焦点，以F为圆心、为半径的圆和抛物线C的准线相交，则的取值范围是

A(0，2)

B[0，2]

C(2，+∞)

D[2，+∞)

正确答案

解析

设圆的半径为r,因为F(0,2)是圆心, 抛物线C的准线方程为,由圆与准线相切知4<r,因为点M(，)为抛物线C：上一点，所以有,又点M(，)在圆 ,所以,所以,即有,解得或, 又因为, 所以, 选C.

的距离为,

知识点

抛物线的标准方程和几何性质

题型：简答题

简答题 · 13 分

某市公租房的房源位于A、B、C三个片区，设每位申请人只申请其中一个片区的房源，且申请其中任一个片区的房源是等可能的，求该市的任4位申请人中：

（1）没有人申请A片区房源的概率；

（2）每个片区的房源都有人申请的概率.

正确答案

（1）（2）

解析

这是等可能性事件的概率计算问题.

（1）所有可能的申请方式有34种，而“没有人申请A片区房源”的申请方式有24种.

记“没有人申请A片区房源”为事件A，则

（2）所有可能的申请方式有34种，而“每个片区的房源都有人申请”的申请方式有

种.

记“每个片区的房源都有人申请”为事件B，从而有

知识点

抛物线的标准方程和几何性质

题型：单选题

单选题 · 5 分

已知P，Q为抛物线x2＝2y上两点，点P，Q的横坐标分别为4，－2，过P，Q分别作抛物线的切线，两切线交于点A，则点A的纵坐标为(　　)

C－4

D－8

正确答案

解析

如图所示，由已知可设

P(4，y1)，Q(－2，y2)，

∵点P，Q在抛物线x2=2y上，

∴

∴P(4,8)，Q(－2,2)，又∵抛物线可化为，∴y′＝x，

∴过点P的切线斜率为，

∴过点P的切线为y－8＝4(x－4)，即

y＝4x－8。

又∵过点Q的切线斜率为，

∴过点Q的切线为y－2＝－2(x＋2)，即y＝－2x－2。

联立解得x＝1，y＝－4，

∴点A的纵坐标为－4

知识点

导数的几何意义抛物线的标准方程和几何性质

题型：单选题

单选题 · 5 分

命题“若p则q”的逆命题是(　　)

A若q则p

B若p则q

C若q则p

D若p则q

正确答案

解析

根据逆命题的定义，命题“若p则q”的逆命题为“若q则p”，故选A项

知识点

抛物线的标准方程和几何性质

题型：单选题

单选题 · 5 分

函数的定义域是（）

正确答案

解析

由题知

解得即

所以该函数的定义域为(2,3)∪(3，＋∞)，故选C。

知识点

抛物线的标准方程和几何性质

题型：简答题

简答题 · 14 分

在平面直角坐标系上，直线：交轴于点，设是上一点，是线段的垂直平分线上一点，且满足。

（1）当点在上运动时，求点的轨迹的方程；

（2）已知，设是上动点，求的最小值，并给出此时点的坐标；

（3）过点且不平行于轴的直线与轨迹有且只有两个不同的交点，求直线的斜率的取值范围。

正确答案

(1) 或 (2) （3）

解析

（1）

如图所示，连接，则

∵，

∴动点满足或在的负半轴上，设

① 当时，，

，化简得

② 当在的负半轴上时，

综上所述，点的轨迹的方程为或

（2）由

（1）知的轨迹是顶点为，焦点为原点的抛物线和的负半轴

① 若是抛物线上的动点，过作于

由于是抛物线的准线，根据抛物线的定义有

则

当三点共线时，有最小值

求得此时的坐标为

② 若是的负半轴上的动点

显然有

综上所述，的最小值为3，此时点的坐标为

（3）如图，

设抛物线顶点，则直线的斜率

∵点在抛物线内部，

∴过点且不平行于轴的直线必与抛物线有两个交点

则直线与轨迹的交点个数分以下四种情况讨论：

① 当时，直线与轨迹有且只有两个不同的交点

② 当时，直线与轨迹有且只有三个不同的交点

③ 当时，直线与轨迹有且只有一个交点

④ 当时，直线与轨迹有且只有两个不同的交点

综上所述，直线的斜率的取值范围是

知识点

抛物线的标准方程和几何性质

题型：单选题

单选题 · 5 分

将两个顶点在抛物线上，另一个顶点是此抛物线焦点的正三角形个数记为，则

正确答案

解析

略

知识点

抛物线的标准方程和几何性质

继续学习学习下一知识点

下一知识点 : 抛物线焦点弦的性质

百度题库 > 高考 > 文科数学 > 抛物线的标准方程和几何性质

扫码查看完整答案与解析