- 抛物线的标准方程和几何性质
- 共169题
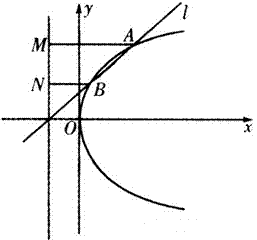
如图,已知直线l:y=k(x+1)(k>0)与抛物线C:y2=4x相交于A、B两点,且A、B两
点在抛物线C准线上的射影分别是M、N,若|AM|=2|BN|,则k的值是
正确答案
解析
略
知识点
设F是抛物线C1:y2=2px (p>0) 的焦点, 点A是抛物线与双曲线C2:
正确答案
解析
由题意,可得点A的横坐标为





知识点
设斜率为2的直线


正确答案
解析
略
知识点
已知抛物线






(1)求抛物线的焦点坐标和准线方程;]
(2)设直线


(3)记点









正确答案
见解析。
解析
(1)抛物线的焦点坐标为
准线方程为:
(2)设



∴


∵


∴
∴
讨论:当

∴直线

令


当



故

(3)由第(2)问可设直线

联立

所以
所以
所以以

当直线



所以


所有
即
所以
又
所以
即



知识点
若抛物线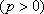
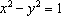
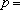
正确答案
2
解析
略
知识点
以抛物y2=4x的焦点为圆心且与双曲线
是____
正确答案
解析
略
知识点
已知抛物线





正确答案
2
解析
略
知识点
抛物线







正确答案
解析
略
知识点
抛物线





正确答案
3
解析
略
知识点
已知抛物线C的顶点在原点,焦点为
(1)求抛物线C的方程;
(2)已知直线




(3)设点




△

正确答案
见解析。
解析
(1)设抛物线C的方程为
由


(2) 设
由


又由

故

解①②③构成的方程组得
又由

所求得的


(3)设

所以直线PR的方程为





同理可得
由于







所以△

知识点
扫码查看完整答案与解析