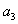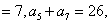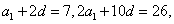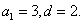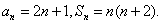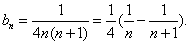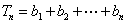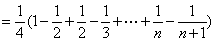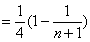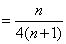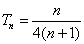- 由数列的前几项求通项
- 共778题
1
题型:填空题
|
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
1
题型:简答题
|
将数列{
……
已知表中的第一列数






(1)求数列{
(2)若上表中从第2行开始,每一行中的数按从左到右的顺序均成等比数列,且公比是同一个正数,已知

正确答案
见解析。
解析
知识点
由数列的前几项求通项等差数列的基本运算错位相减法求和
1
题型:简答题
|
已知等差数列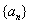
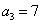
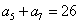
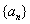
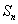
(1) 求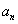
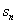
(2) 令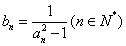
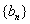
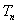
正确答案
见解析。
解析
(1)设等差数列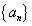
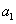
由于
所以
解得
由于
(2)因为 
因此
故
所以数列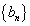
知识点
由数列的前几项求通项等差数列的性质及应用等差数列的前n项和及其最值裂项相消法求和
1
题型:简答题
|
(1)设

(2)

正确答案
见解析
解析
本题考查不等式的性质,对数函数的性质和对数换底公式等基本知识,考查代数式的恒等变形和推理论证能力。
证明:(1)由于x≥1,y≥1,所以
将上式中的右式减左式,得
既然x≥1,y≥1,所以
(2)设
于是,所要证明的不等式即为
其中
故由(1)立知所要证明的不等式成立。
知识点
由数列的前几项求通项
1
题型:简答题
|
已知数列






(1)求
(2)求证:在数列


(3)求数列
正确答案
见解析。
解析
(1) 
(2) ① 任意


② 假设
∴ 在数列


(3) 


∵
知识点
由数列的前几项求通项等差数列的基本运算
下一知识点 : 由an与Sn的关系求通项an
扫码查看完整答案与解析