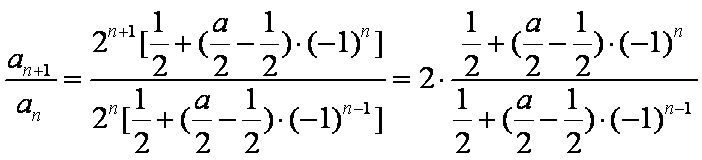
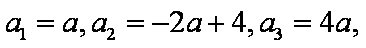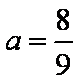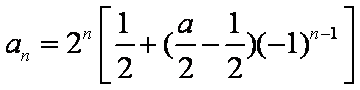- 由数列的前几项求通项
- 共778题
数列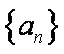
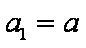
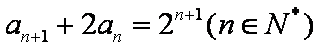
(1)若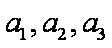
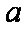
(2)数列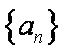
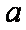
正确答案
见解析
解析
(1)
因为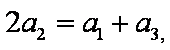
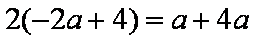
(2)因为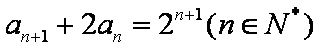
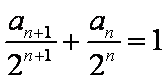
得: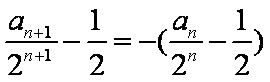
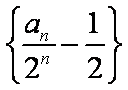
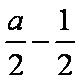
所以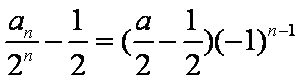
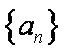
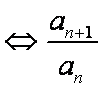
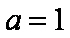
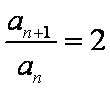
知识点
已知数列



正确答案
解析





代入检验知n的最小值是10,故选C。
知识点
在等差数列







(1)求数列

(2)设






正确答案
见解析
解析
(1)设等差数列



由题意,得

∴

(2)
∴
∴
∴

令


故


知识点
已知数列



(1)设



(2)求数列

正确答案
见解析
解析
(1)方法1:假设存在实数


由




所以


所以


当



有
当



有
所以存在实数

当



当



方法2:假设存在实数

设


与已知



所以存在实数

当



当



(2)解法1:由(1)知
当



当


故数列

解法2:由(1)可知,

则
当

当

故数列

若将上述和式合并,即得
知识点
已知数列







(1)求数列
(2)已知





正确答案
见解析
解析
(1)
(2)
若




令
所以
知识点
已知等差数列






正确答案
答案:
解析
解法1:运用线性规划的知识可得整数点
解法2:运用不等式的知识可得
解法3:猜测也可以
知识点
给定有限单调递增数列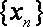
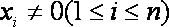
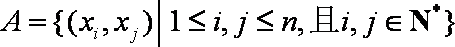
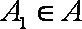
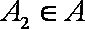
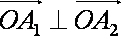
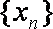
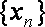
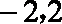
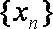
①数列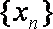
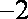
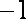
②若数列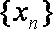
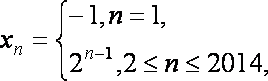
③若数列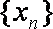
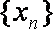
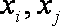
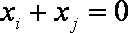
其中正确的是
正确答案
解析
对于①,取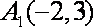
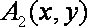
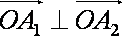
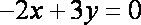
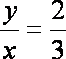
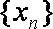
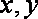
对于②,取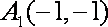
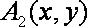
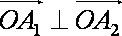
对于③,取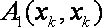
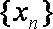
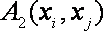
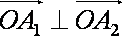
即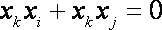

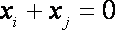
知识点
已知数列



(1)求数列
(2)记



正确答案
见解析
解析
本题考查数列等基本知识,考查推理论证能力和运算求解能力,考查函数与方程的思想、化归与转化的思想。
(1)因为


因为
所以
两式相减得
所以
所以
(2)



知识点
已知无穷数列



(1)若m=12,求
(2)若
(3)记


正确答案
见解析。
解析
(1)
(2) 





(3)
m=1,2,3时,有
下面证明 
又

知识点
已知数列{an}满足an•an+1•an+2•an+3=24,且a1=1,a2=2,a3=3,则a1+a2+a3+…+a2013= 。
正确答案
5031
解析
依题意可知,an•an+1•an+2•an+3=24,以n+1代n,得出an+1•an+2•an+3•an+4=24,两式相除可推断出an+4=an,
∴数列{an}是以4为周期的数列,
求得a4=4
∴S2013=503×(1+2+3+4)+1=5031
知识点
扫码查看完整答案与解析