由数列的前几项求通项
共778题

· 由数列的前几项求通项

由数列的前几项求通项
共778题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

已知等差数列{}满足，.

（1）求数列{}的通项公式；

（2）求数列的前项和。

正确答案

见解析

解析

解：

（1 ）设等差数列的公差为d，由已知条件可得

解得

故数列的通项公式为

（2）设数列，即，

所以，当时，

所以

综上，数列

知识点

由数列的前几项求通项

题型：填空题

填空题 · 5 分

12.已知数列的通项公式为，则=（）

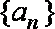
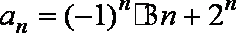
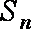
正确答案

解析

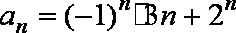
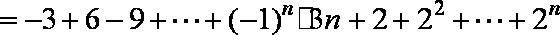
因为，所以，

当n为奇数时，，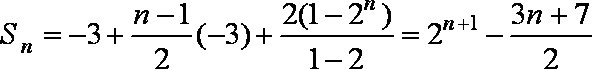

当n为偶数时，.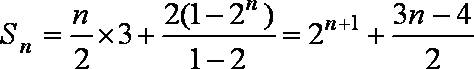

知识点

由数列的前几项求通项

题型：填空题

填空题 · 5 分

15.把正偶数依次按如下规律进行排序：第一个括号括一个数，第二个括号括两个数，第三个括号括三个数，第四个括号括一个数，…，依次循环，如（2）,（4,6）,（8,10,12）,（14），…，则第50个括号内的各数的和为（）

正确答案

394

解析

由题意可知，每三个括号将用掉数列的6项，所以前49个括号共用了数列的97项，第50个括号里有两个数分别是196和198，故两个数的乘积为394.

知识点

由数列的前几项求通项

题型：简答题

简答题 · 7 分

已知矩阵A的逆矩阵A﹣1=。

（1）求矩阵A；

（2）求曲线xy=1在矩阵A所对应的线性变换作用下所得的曲线方程。

正确答案

见解析。

解析

（1）因为矩阵A是矩阵A﹣1的逆矩阵，

且，

所以。

（2）设xy=1上任意一点（x，y）在矩阵A所对应的线性变换作用下的像为点（x′，y′），

则，

由此得，

代入方程xy=1，得y′2﹣x′2=2。

所以xy=1在矩阵A所对应的线性变换作用下的曲线方程为y2﹣x2=2.

知识点

由数列的前几项求通项

题型：单选题

单选题 · 5 分

在等差数列{an}中，若a2=1，a8=2a6+a4，则a5的值是（　　）

A﹣5

正确答案

解析

设等差数列{an}的公差为d，

∵a2=1，a8=2a6+a4，

∴a1+d=1，a1+7d=2（a1+5d）+a1+3d

联立解得a1=，d=﹣，

∴a5=a1+4d=+4（﹣）=

故选：B

知识点

由数列的前几项求通项

题型：简答题

简答题 · 12 分

设数列的前项和为，且，其中是不为零的常数。

（1）证明：数列是等比数列；

（2）当时，数列满足，，求数列的通项公式。

正确答案

见解析

解析

（1）证明：因为,则，

所以当时，，整理得，

由，令，得，解得。

所以是首项为，公比为的等比数列，

（2）当时，由（1）知，则，

由，得，

当时，可得

＝，

当时，上式也成立。

∴数列的通项公式为，

知识点

由数列的前几项求通项

题型：简答题

简答题 · 14 分

18.正项数列满足.

（1）求出的通项公式；

（2）若数列前n项和为，求证：；

（3）若数列满足，求数列的前n项和

正确答案

见解析。

解析

（1），

所以或(舍)，所以的通项公式

（2）利用数学归纳法证明：因为，当n=1时显然成立。

假设当n=k时成立，即，

所以当n=k+1时，

，即当n=k+1时也成立

所以对任意正整数n，都成立。

（3）因为，，所以，

所以

知识点

由数列的前几项求通项

题型：简答题

简答题 · 12 分

已知数列满足:，.

（1）证明数列为等差数列；

（2）求数列的通项公式及其前项和.

正确答案

见解析。

解析

（1）证明：由已知，当时，①，②，

① - ②可得，又，所以成等差数列。

所以数列是以1为首项，2为公差的等差数列

（2）由（1）知为奇数时，则为偶数时，,得，

所以

为偶数时，

为奇数时，

又

故

知识点

由数列的前几项求通项

题型：填空题

填空题 · 5 分

17.已知，是非零向量，则下列说法正确的有____.

①，则的最大值为；

②若，则；

③若，则，的夹角为；

④是，的夹角为锐角的充要条件；

⑤，，成等差数列是，共线的必要不充分条件。

正确答案

①

解析

①因为，所以，又，所以，要求最大值，则，所以，所以的最大值为，所以说法正确；

②若，运用向量加法的三角形法则，可知，以，，为边的三角形是等腰三角形，，是三角形的两腰，为一底，所以与的大小不确定，故说法错误;

③

因为即，即，结合余弦函数图像可得，，故说法错误；

④

根据向量加法的平行四边形法则可知和是以，为邻边的平行四边形对角线长，且，即，即，即，所以，但是，的夹角可能为0，所以是，的夹角为锐角的必要不充分条件，故说法错误；⑤，，成等差数列，即，即，所以，所以或，所以，，成等差数列是，共线的既不充分也不必要条件.故⑤说法错误确. 综上可得正确的是①。

知识点

由数列的前几项求通项

题型：填空题

填空题 · 5 分

13.已知数列的通项公式为，则= .

正确答案

解析

因为，所以，

当n为奇数时，，

当n为偶数时，.

知识点

由数列的前几项求通项

继续学习学习下一知识点

下一知识点 : 由an与Sn的关系求通项an

百度题库 > 高考 > 理科数学 > 由数列的前几项求通项

扫码查看完整答案与解析