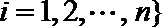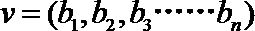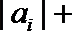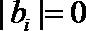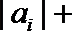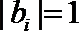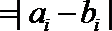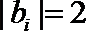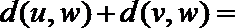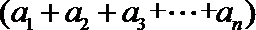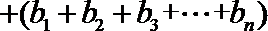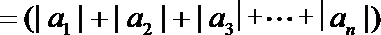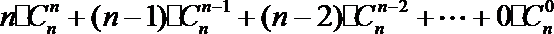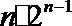- 由数列的前几项求通项
- 共778题
1
题型:
单选题
|
17.若矩阵


正确答案
D
解析
解析已在路上飞奔,马上就到!
知识点
由数列的前几项求通项
1
题型:简答题
|
20.已知
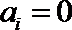
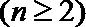
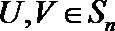
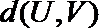
(Ⅰ)令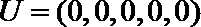
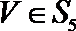
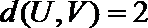
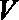
(Ⅱ)令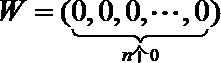
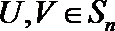
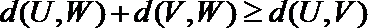
(Ⅲ)给定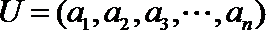
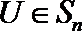
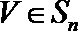
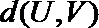
正确答案
解:(Ⅰ)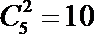
(Ⅱ)证明:令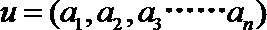
∵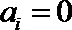
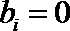
当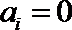
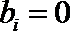
当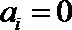
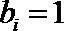
当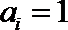
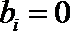
当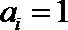
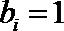
故
∴
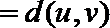
(Ⅲ)解:易知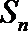
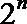
∵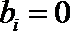
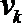
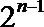
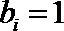
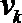
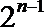
∴
=
=
∴
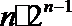
法二:根据(Ⅰ)知使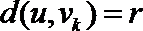
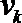
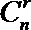
∴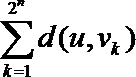
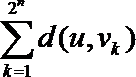
两式相加得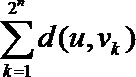
解析
解析已在路上飞奔,马上就到!
知识点
由数列的前几项求通项
1
题型:简答题
|
19.已知


(1)求数列
(2)记






正确答案
(1)由


代入
(2)
化简可得:


解析
解析已在路上飞奔,马上就到!
知识点
由数列的前几项求通项等差数列的基本运算等差数列与等比数列的综合
1
题型:简答题
|
16.已知数列






(1)求数列

(2)设




正确答案
(1)由


所以数列

于是

当
当


又



(2)由(Ⅰ)知



所以
等式两边同乘以

(1)-(2)得
所以
解析
解析已在路上飞奔,马上就到!
知识点
由数列的前几项求通项
1
题型:简答题
|
17.设等差数列

(1)若

(2)若

正确答案
(1)由
又
故解得
因此,

(2)由
即
由①+②得-7d<11,即
由①+③得

于是


将4代入①②得
又
所以,所有可能的数列

解析
解析已在路上飞奔,马上就到!
知识点
由数列的前几项求通项等差数列的基本运算等差数列的前n项和及其最值
下一知识点 : 由an与Sn的关系求通项an
扫码查看完整答案与解析