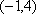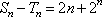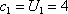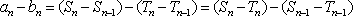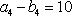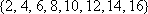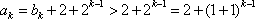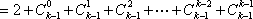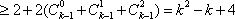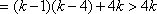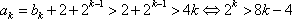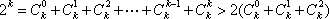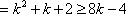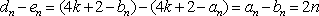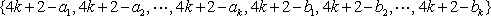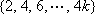- 由数列的前几项求通项
- 共778题
1
题型:简答题
|
已知数列


(1)求

(2)设


正确答案
见解析。
解析
(1)设


解得

所以
(2)∵
∴
∴
知识点
由数列的前几项求通项
1
题型:填空题
|
已知数列







正确答案
1,
解析
略
知识点
由数列的前几项求通项
1
题型:填空题
|
把三阶行列式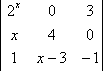
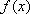

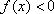
正确答案
解析
略
知识点
由数列的前几项求通项
1
题型:填空题
|
已知数列



正确答案
解析
略
知识点
由数列的前几项求通项
1
题型:简答题
|
设项数均为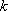
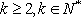
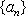
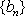
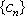

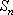
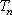
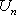
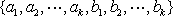
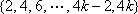
(1)已知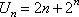
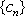
(2)若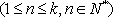
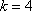
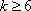
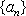
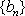
(3)若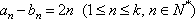
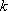
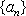
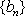
正确答案
见解析
解析
解析:(1)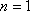
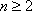
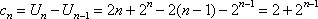
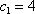
故,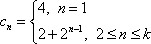
(2)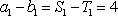
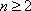
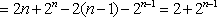
当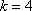
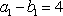
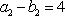
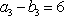
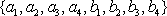
数列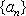
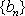
① 6,12,16,14;2,8,10,4 ② 16,10,8,14;12,6,2,4 …………………8分
当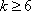
此时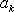
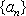
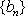
另证:
当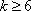
(3)令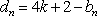
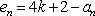
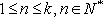
又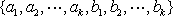
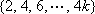
=
所以,数列对(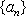
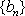
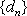
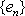
假设数列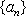
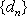
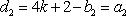
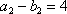
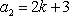
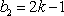
故,符合条件的数列对(
知识点
由数列的前几项求通项
下一知识点 : 由an与Sn的关系求通项an
扫码查看完整答案与解析