- 弧度与角度的互化
- 共37题
若向量









正确答案
解析
由题意可得,(






(2





则|

故选:B。
知识点
设双曲线


正确答案
解析
由双曲线方程可知渐近线方程为

知识点
已知正方体ABCD-A'B'C'D'的棱长为1,点M是棱AA'的中点,点O是对角线BD'的中点。
(1)求证:OM为异面直线AA'和BD'的公垂线;
(2)求二面角M-BC'-B'的大小;
(3)求三棱锥M-OBC的体积。
正确答案
见解析。
解析
知识点
在平面直角坐标系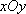
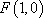

(1)求轨迹为C的方程
(2)设斜率为k的直线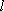
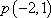
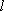
正确答案
见解析。
解析
(1)设M(x,y),依题意得:|MF|=|x|+1,即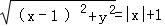
化简得,y2=2|x|+2x。
∴点M的轨迹C的方程为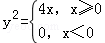
(2)在点M的轨迹C中,记C1:y2=4x(x≥0),C2:y=0(x<0)。
依题意,可设直线l的方程为y﹣1=k(x+2)。
由方程组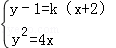
①当k=0时,此时y=1,把y=1代入轨迹C的方程,得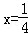
故此时直线l:y=1与轨迹C恰好有一个公共点(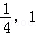
②当k≠0时,方程ky2﹣4y+4(2k+1)=0的判别式为△=﹣16(2k2+k﹣1)。
设直线l与x轴的交点为(x0,0),
则由y﹣1=k(x+2),取y=0得
若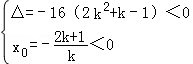
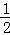
即当k∈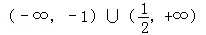
故此时直线l与轨迹C恰好有一个公共点。
若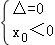
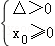
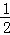
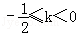
即当k=﹣1或k=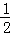
当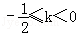
故当k=﹣1或k=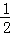

若
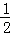
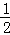
即当﹣1<k<﹣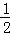
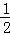
此时直线l与C恰有三个公共点。
综上,当k∈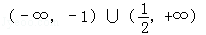
当k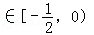
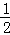
当k∈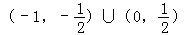
知识点
6个人排成一行,其中甲、乙两人不相邻的不同排法共有__________种,(用数字作答)
正确答案
480
解析
先排除甲、乙外的4人,方法有


知识点
扫码查看完整答案与解析






