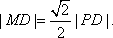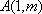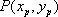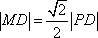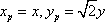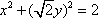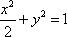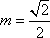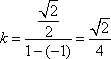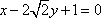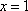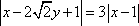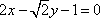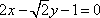- 定义法求轨迹方程
- 共97题
已知平面内一动点 P到定点

(1)求动点 P的轨迹C的方程;
(2)当点 P(x0,y0)(x0≠0)在(1)中的轨迹C上运动时,以 M P为直径作圆,求该圆截直线
(3)当点 P(x0,y0)(x0≠0)在(1)中的轨迹C上运动时,过点 P作x轴的垂线交x轴于点 A,过点 P作(1)中的轨迹C的切线l交x轴于点 B,问:是否总有 P B平分∠A PF?如果有,请给予证明;如果没有,请举出反例。
正确答案
见解析。
解析
(1)根据题意,动点 P是以

所以p=1开口向上,
所以动点 P的轨迹C的方程为x2=2y
(2)以 M P为直径的圆的圆心(


所以圆的半径r=



故截得的弦长l=2

(3)总有 P B平分∠A PF。
证明:因为
所以,y′=x,
所以切线l的方程为
令y=0得
所以B(
所以B到PA的距离为
下面求直线PF的方程,
因为
所以直线PF的方程为
所以点B到直线PF的距离
所以 PB平分∠APF。
知识点
设函数

(1)当


(2)如果存在


(3)如果对任意的


正确答案
见解析。
解析
(1)当


所以曲线

(2)

考虑
由上表可知,
所以满足条件的最大整数
(3)对任意的




有(2)知,在区间



记
记




当


即函数


所以

知识点
已知椭圆










(1)求曲线
(2)设点




(3)设






正确答案
见解析
解析
(1)解:依题意可得

设双曲线

因为双曲线的离心率为


所以双曲线

(2)证法1:设点







则直线

联立方程组
整理,得
解得


同理可得,
所以
证法2:设点




则

因为


因为点



即

所以

所以
证法3:设点


联立方程组
整理,得
解得
将



所以
(3)解:设点




则

因为


因为点



因为点

因为

所以
由(2)知,

设


设

当



所以函数


因为

所以当


当


所以

知识点
如图,设P是圆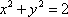
(1)当点P在圆上运动时,求点M的轨迹C的方程;
(2)已知点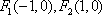
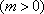
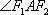
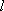
正确答案
见解析。
解析
(1)设点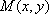
∵点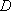
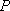

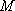
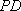
∴
∵点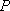

整理得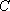
(2)由(1)知点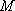
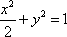
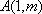
∴直线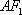
故直线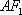
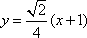
由题意知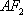
由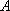
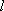
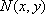
则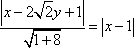
若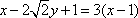
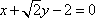
于是由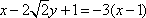
故直线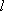
知识点
已知:曲线


(1)求曲线
(2)过点






(3)设







正确答案
见解析
解析
(1)
(2)当直线
当直线


得
记






(3)将

记







知识点
扫码查看完整答案与解析