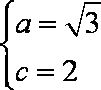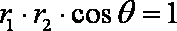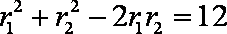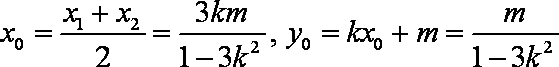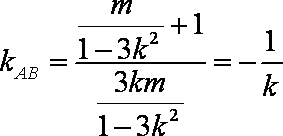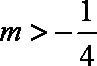- 定义法求轨迹方程
- 共97题
已知函数

(1)当


(2)当

(3)证明:对任意的
正确答案
见解析。
解析
(1)解:当





(2)解:


因为
(1)若

所以,


………………………………8分
(2)若


所以,

………………………………10分
(3)证明:由(2)可知,当



(1)当

所以对任意
(2)当



所以
若


所以,对任意
综上,对任意
知识点
设椭圆C1和抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表中:
(1)求曲线C1,C2的标准方程;
(2)设直线



正确答案
见解析。
解析
(1)由题意(-2,0)一定在椭圆C1上。设C1方程为
则

所以



从而


(2)假设直线
当
此时
当




设







知识点
已知函数
(1)当t=1时,求曲线
(2)当t≠0时,求的单调区间;
(3)证明:对任意的
正确答案
见解析。
解析
(1)当t=1时,
(2)
因为t≠0,以下分两种情况讨论:
①若
所以,



②若
所以,



综上可得:
当t<0时,


当t>0时, 



(3)由(2)可知,当t>0时,


①当
所以对任意
②当



知识点
已知双曲线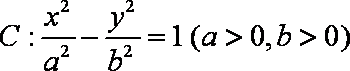
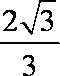
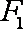
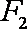
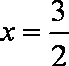
(1)求双曲线
(2)若双曲线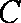
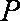
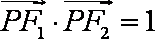

(3)若直线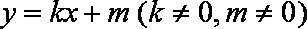

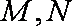
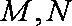
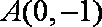

正确答案
见解析。
解析
(1)由条件有
∴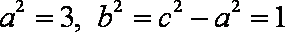
故双曲线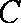
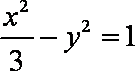
(2)设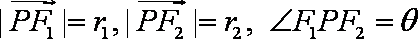
∵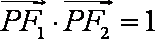
又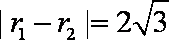
即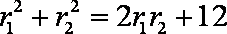
又由余弦定理有:
即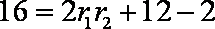
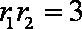
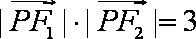
(3)由
则由条件有: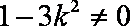
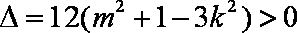
设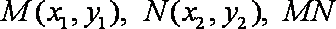
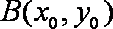
又
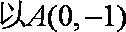

化简得: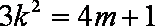
将②代入①得: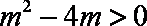
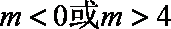
又由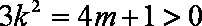
综上: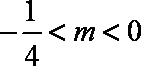

知识点
已知曲线



(1)求曲线
(2)设过







正确答案
见解析。
解析
(1)根据椭圆的定义,可知动点


则

(2)当直线

当直线








∴
∴ 
得


代入①,得
即


所以,直线


知识点
扫码查看完整答案与解析