· 曲线与方程

· 定义法求轨迹方程

定义法求轨迹方程
共97题

· 曲线与方程

· 定义法求轨迹方程

定义法求轨迹方程
共97题

热门试卷

X 查看更多试卷

1

题型：简答题

|

简答题 · 13 分

21．在平面直线坐标系XOY中，给定两点A（1，0），B（0，-2），点C满足，其中，且。

（1）求点C的轨迹方程；

（2）设点C的轨迹与双曲线（）相交于M，N两点，且以MN为直径的圆经过原点，求证：是定值；

（3）在（2）条件下，若双曲线的离心率不大于，求该双曲线实轴的取值范围。

正确答案

（1）设C（）则

（2）设M（）

N（）则，

韦达定理代入得

（定值）

（3）

又

代入得

解析

解析已在路上飞奔，马上就到！

知识点

定义法求轨迹方程

1

题型：简答题

|

简答题 · 16 分

19．已知函数（）的图象为曲线。

（1）求曲线上任意一点处的切线的斜率的取值范围；

（2）若曲线上存在两点处的切线互相垂直，求其中一条切线与曲线的切点的横坐标的取值范围；

（3）试问：是否存在一条直线与曲线C同时切于两个不同点？如果存在，求出符合条件的所有直线方程；若不存在，说明理由。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

定义法求轨迹方程

1

题型：简答题

|

简答题 · 16 分

18．已知曲线C：.

（1）证明：不论取何实数，曲线C必过定点；

（2）当时，若曲线C与直线相切，求的值.；

（3）对所有的且，是否存在直线与曲线C总相切？如果存在，求出的方程；如果不存在，请说明理由。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

定义法求轨迹方程

1

题型：填空题

|

填空题 · 5 分

3．若曲线在点处的切线平行于直线，则点的坐标为（）

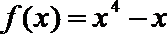
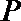
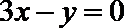
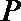
正确答案

（1，0）

解析

解析已在路上飞奔，马上就到！

知识点

定义法求轨迹方程

1

题型：简答题

|

简答题 · 14 分

21．如图，已知椭圆的左右焦点分别为．，椭圆的下顶点为，点是椭圆上任意一点，圆是以为直径的圆。

（1）若圆过原点，求圆的方程；

（2）当圆的面积为时，求所在直线的方程；

（3）写出一个定圆的方程，使得无论点在椭圆的什么位置，该定圆总与圆相切,请写出你的探究过程．

正确答案

（1）解法一：因为圆过原点，所以，所以是椭圆的端轴顶点，的坐标是或，于是点的坐标为或，

圆的方程为或。

解法二：设，因为圆过原点，所以，

所以，所以，，点

于是点的坐标为或，

圆的方程为或。

（2）设圆的半径为，由题意，，，所以

设，则。联立，解得（舍去），

所以点或．所以或，

所以直线的方程为或

（3）以原点为圆心，为半径的定圆始终与圆相内切。定圆的方程为

探究过程为：设圆的半径为，定圆的半径为，

因为，

所以当原点为定圆圆心，半径时，定圆始终与圆相内切。

解析

解析已在路上飞奔，马上就到！

知识点

定义法求轨迹方程

继续学习学习下一知识点

下一知识点 : 相关点法求轨迹方程

百度题库 > 高考 > 文科数学 > 定义法求轨迹方程

扫码查看完整答案与解析