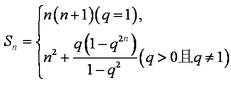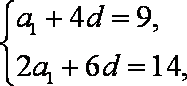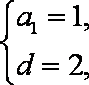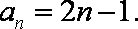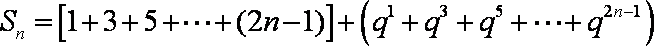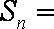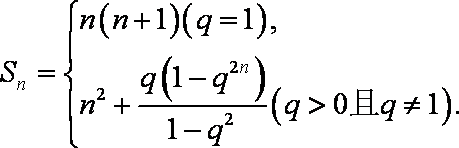- 由数列的前几项求通项
- 共480题
已知公差不为零的等差数列




(1)求数列
(2)设


正确答案
(1)an=2n-1(2)Sn
解析
(1)设


∵



又



∴

(2)∵
∴
知识点
已知数列




(1)求数列

(2)求数列


正确答案
见解析
解析
(1)


数列
由

(2)
知识点
如图所示,程序框图的功能是
正确答案
解析
循环共进行10次,得到
知识点
已知等差数列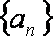

(1)求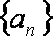
(2)若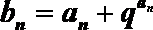
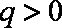
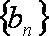
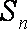
正确答案
(1)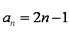
解析
解析:(1)设
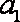
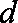
由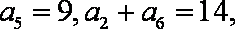
解得
所以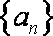
(2)由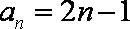
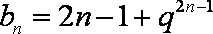
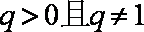
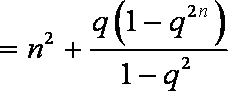
② 当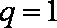
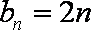
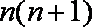
所以数列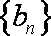
知识点
数列








(1)证明:数列

(2)若


正确答案
见解析。
解析
(1)
又


又



当




(2)


=
=





知识点
已知数列



(1)求数列
(2)设





正确答案
见解析
解析
(1)由已知,


即



∴数列

∴
(2)∵


∴
∴
∴
(ⅰ)当

当且仅当

∴
(ⅱ)当

当且仅当


∴
即


综上所述,存在


知识点
等差数列




(1)求数列
(2)设

正确答案
(1)an=n(2)
解析
(1)由

又



(2)根据(1)得

由于函数


而


所以当


即数列

知识点
已知数列

(1)求数列
(2)求证:
正确答案
见解析
解析
(1)设等差数列的公差为d,
由

所以

(2)证明:
所以
知识点
已知数列


(1)求证:数列

(2)若数列



正确答案
(1)an=2n-1(2)Sn=
解析
(1)

又



∴数列


(2)∵

∴
即

知识点
巳知等比数列{an}的首项和公比都为2,且a1,a2分别为等差数列{bn}中的第一、第三项。
(1)求数列{an}、{bn}的通项公式;
(2)设Cn=
正确答案
见解析。
解析
(1)∵等比数列{an}的首项和公比都为2,
∴
∵a1,a2分别为等差数列{bn}中的第一、第三项
∴b1=2,b3=4
∴bn=n+1;
(2)设Cn=

∴Sn=


知识点
扫码查看完整答案与解析