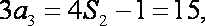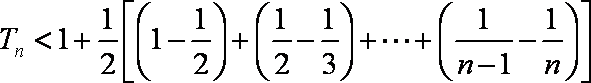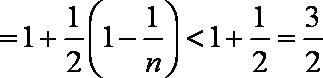- 由数列的前几项求通项
- 共480题
已知数列{



正确答案
解析
由





知识点
已知在等比数列




(1)求数列
(2)若数列




正确答案
见解析
解析
(1)设公比为q,则





(2)
则
知识点
已知



(1)求证:数列
(2)是否存在正整数

正确答案
见解析
解析
(1)由题意,

由两式相减,得
即

又

∴数列


(2)由(1)得
又由


∵


知识点
19.已知数列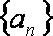
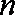
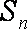
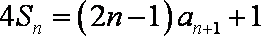
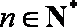
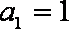
(1)求证:数列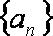
(2)设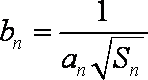
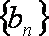
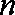
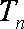
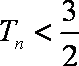
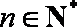
正确答案
见解析。
解析
(1)由题设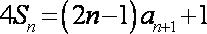
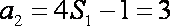
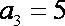
当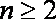
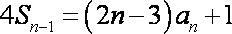
两式相减得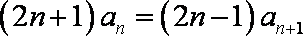
方法一:由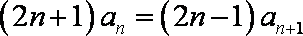
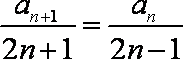

则数列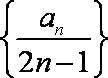
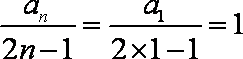
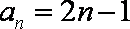
所以数列
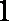
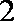
方法二:由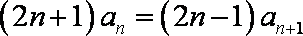
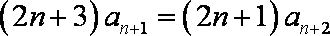
两式相减得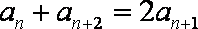
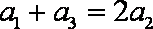
所以数列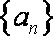
(2)由(Ⅰ)得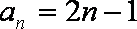
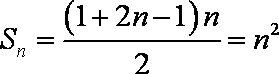
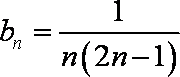
当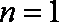
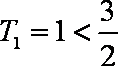
当
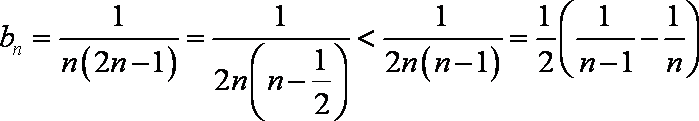
所以
综上所述,命题得证。
知识点
11.已知数列



正确答案
26
解析
略。
知识点
14.已知曲线C1与C2的极坐标方程分别为 


正确答案
解析
略。
知识点
在某市的人大贿选案中,经调查统计该市人大代表的受贿情况的频率分布直方图如下:其中受贿[10,20]万元的有10人,请探究在这次贿选案该市人大代表中有多少人没有受贿,及这次贿选案中人均受贿多少万元。
正确答案
没有受贿的人数:6人;平均受贿金额:27.9万元
解析
人大代表人数
没有受贿的人数:

平均受贿金额:

知识点
已知


(1)求数列
(2)若数列


求数列


正确答案
见解析。
解析
(1)设等差数列

由

由

易得

备注:也可以由


(2)令





而

于是
=

知识点
已知数列







(1)求

(2)设



正确答案
见解析。
解析
(1)当


当


①-②,得

故


故
由



因


解得


(2)由(1),得
所以




③-④,得


=6+


所以

知识点
科拉茨是德国数学家,他在1937年提出了一个著名的猜想:任给一个正整数n,如果n是偶数,就将它减半(即

(1)如果
(2)如果对正整数

正确答案
(1)1
(2)6
解析
(1)如果n=2,按以上变换规则,得到数列:a1=2,a2=1,a3=4,…,a8=1;
(2)设对正整数n按照上述变换,得到数列:a1,a2,…,a7,a8,
∵a8=1,则a7=2
则n的所有可能取值为2,3,16,20,21,128,共6个。
知识点
扫码查看完整答案与解析