- 等差数列与等比数列的综合
- 共59题
23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分
若无穷数列




(1) 若







(2) 若无穷数列






(3) 设





正确答案
(1)
∴
∴
∴
∴
∴
(2)设



∴
∴
∴
∴
∴
∵
而

故
(3) 充分性:若
则
若存在

则
故
必要性:若对任意

则
设函数
由

∴一定能找到一个
∴
∴
故
∴
知识点
18.(本小题满分12分)
已知数列

(Ⅰ)求数列
(Ⅱ)另

正确答案
知识点
已知


17.求数列
18.记




正确答案
(1)
解析
(Ⅰ)设数列

解得
所以
考查方向
解题思路
利用等差数列的基本量的运算求解即可;
易错点
利用等差数列的基本量求通项公式时运算出错;
正确答案
(2)2
解析
(Ⅱ)由(Ⅰ)可得
∴

因 


即 



∴
考查方向
解题思路
根据公式先求

易错点
不会转化题中的条件 
设等差数列





20.求数列

21.当



正确答案
(Ⅰ)

解析
(Ⅰ)由题意有,


故

考查方向
解题思路
(Ⅰ)由已知可列出方程组
易错点
公式记错。
正确答案
(Ⅱ)
解析
由





①-②可得

故
考查方向
解题思路
(Ⅱ)由(Ⅰ)可得



易错点
不知道用错位相减法求和。
20.设数列








(1)若数列


(2)若数列



(3)试构造一个数列





正确答案
(1)

(2)

(3)
解析
试题分析:本题属于数列综合问题,题目的难度是逐渐由易到难,(1)(2)直接按照单调数列定义来求(3)构造新数列时,要把握问题的本质。
(1)因为


所以

(2)根据题意可知,


可得



则




所以


(3)构造


下证数列
证明:因为

所以

所以

因为
所以数列
考查方向
解题思路
解决等差数列与等比数列的综合问题,关键是理清两个数列的关系。解综合问题的成败在于审清题意,通过给定信息的表象,抓住问题的本质,揭示问题的内在联系与隐含条件。
易错点
1、数列单调性的巧妙运用。
2、第三问中构造不正确得不到正确结论。
知识点
已知各项均不相等的等差数列



22.求数列


23.是否存在正整数

正确答案
见解析
解析
考查方向
解题思路
借助等差数列前4项和,与
解析式
易错点
本题易错于裂项等号不成立,第二问不理解题意
正确答案
见解析
解析
考查方向
解题思路
根据等比数列性质写出关系式
解不等式确定取值
易错点
本题易错于裂项等号不成立,第二问不理解题意
5.公差为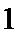
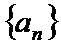
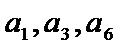
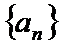
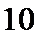
正确答案
解析
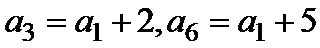
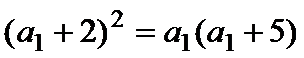
解得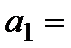
所以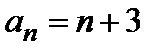
考查方向
解题思路
根据等差数列的定义,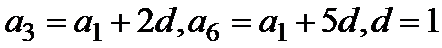
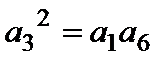

易错点
不知道等比中项的性质,或把等比中项与等差中项混淆
知识点
3.在各项均为正数的等比数列



正确答案
解析
由







考查方向
本题主要考查数列的通项公式、等差中项、前n项和等知识,意在考生的运算推理能力。
解题思路
1.先根据

2.然后利用等比数列的求和公式求出
易错点
1.不会转化
2.误用等差数列求等比数列的前n项和。
知识点
17.在公比为




(Ⅰ)求
(Ⅱ)若函数








正确答案
(Ⅰ)
(Ⅱ)
解析
试题分析:本题属于数列和三角函数中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求(2)要注意图像的应用.
(Ⅰ) 解:由题可知

故
(Ⅱ)∵点

∴
又∵
如图,连接

又∵
∴
∴
考查方向
本题考查了数列与三角函数的知识,涉及到等比数列及三角函数的应用,是高考题中的高频考点.
解题思路
本题考查数列与三角函数的知识,解题步骤如下:
1、利用通项公式求解。
2、利用函数图像性质代入求解。
易错点
三角函数图像易错。
知识点
20.某农场规划将果树种在正方形的场地内。为了保护果树不被风吹,决定在果树的周围种松树。 在下图里,你可以看到规划种植果树的列数(n),果树数量及松树数量的规律:
(1)按此规律,n = 5时果树数量及松树数量分别为多少;并写出果树数量

(2)定义:


正确答案
(1)n = 5时果树25棵,松树40棵;

(2)
当
当
解析
(1)观察图例可以看出规划种植果树的列数(n),果树数量及松树数量的规律:果树的数量总等于n的平方,每条边上松树的数量总比前一个多两棵,四条边共多出八棵,满足等差数列的规律。由此可得:n = 5时果树25棵,松树40棵
(2)由题意和第一问得到的通项公式可得:
所以当
当
考查方向
解题思路
本题考查了观察归纳法求数列通项的基本能力,为了观察方便,可以把松树的变化规律先分解到四条边上分别考虑。
易错点
本题必须注意项数和项的值之间的关系,忽视则会出现错误。
知识点
扫码查看完整答案与解析