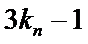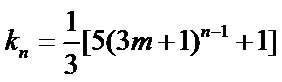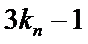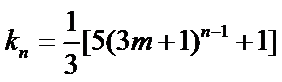- 等差数列与等比数列的综合
- 共59题
等差数列


17.求数列

18.设

正确答案
见解析
解析
设等差数列







考查方向
解题思路
第一问根据前N项和求通项公式,第二问用裂项相消的办法求数列的和
易错点
相关性质掌握不好;不会求数列的和
正确答案
见解析
解析
由(1)得
考查方向
解题思路
第一问根据前N项和求通项公式,第二问用裂项相消的办法求数列的和
易错点
相关性质掌握不好;不会求数列的和
已知等差数列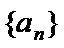
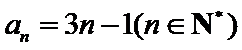
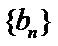
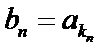
若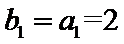
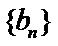
28.写出数列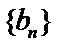
29.求数列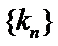
30.证明:以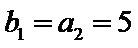
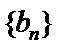
正确答案
2,8,32,128.
解析
试题分析:本题属于数列通项公式与数列求和公式的应用问题,由于问题较抽象有一定的难度。(1)求解时一定要灵活应用数学归纳法对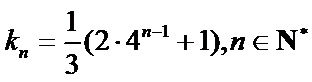
(Ⅰ)观察数列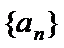
因为数列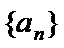
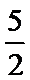
(ⅰ)以2为首项,且公比最小的等比数列的前四项是2,8,32,128.
(ⅱ)由(ⅰ)可知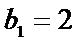
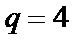
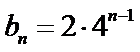
又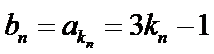
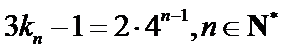
即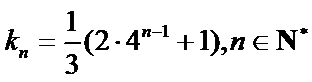
再证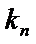
显然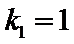
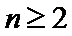
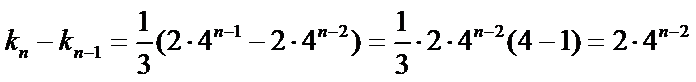
即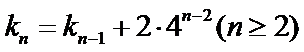
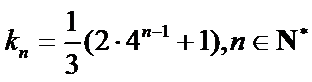
所以,所求通项公式为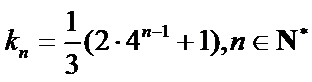
考查方向
解题思路
本题考查了等差等比数列通项公式的求解,数列求和公式的综合应用,数学归纳法和分析法的应用,解题步骤如下:
(ⅰ)根据题意写出数列的前四项是2,8,32,128.;(ⅱ)根据题意写出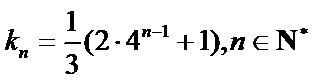
在证明“以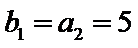
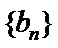
易错点
由题归纳法得数列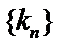
正确答案
an=22n-1;
解析
试题分析:本题属于数列通项公式与数列求和公式的应用问题,由于问题较抽象有一定的难度。(1)求解时一定要灵活应用数学归纳法对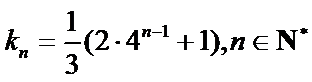
(Ⅱ)设
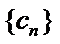
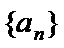
且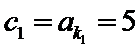
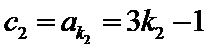
所以公比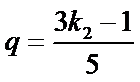
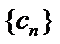
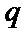
取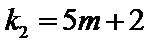
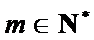
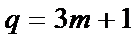
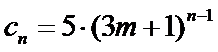
只要证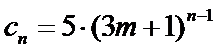
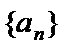
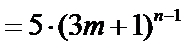
只要证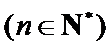
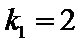
又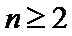
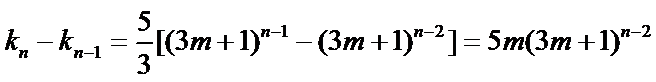
即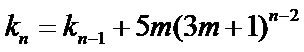
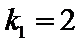
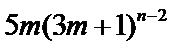

故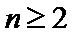
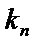
所以数列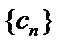
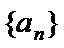
其公比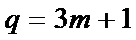
故数列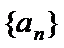
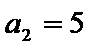
考查方向
解题思路
本题考查了等差等比数列通项公式的求解,数列求和公式的综合应用,数学归纳法和分析法的应用,解题步骤如下:
(ⅰ)根据题意写出数列的前四项是2,8,32,128.;(ⅱ)根据题意写出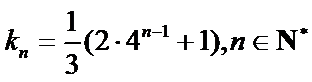
在证明“以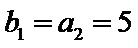
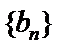
易错点
由题归纳法得数列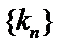
正确答案
证明略。
解析
试题分析:本题属于数列通项公式与数列求和公式的应用问题,由于问题较抽象有一定的难度。(1)求解时一定要灵活应用数学归纳法对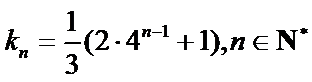
(Ⅱ)设
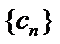
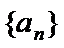
且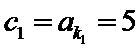
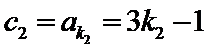
所以公比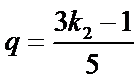
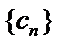
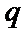
取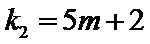
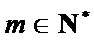
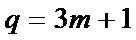
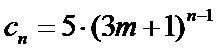
只要证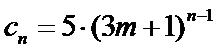
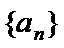
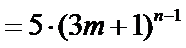
只要证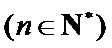
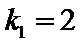
又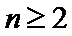
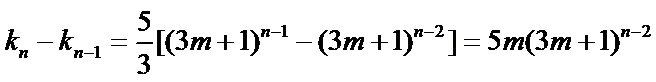
即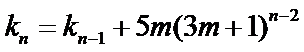
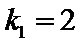
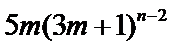

故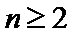
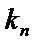
所以数列
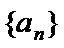
其公比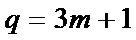
故数列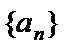
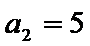
考查方向
解题思路
本题考查了等差等比数列通项公式的求解,数列求和公式的综合应用,数学归纳法和分析法的应用,解题步骤如下:
(ⅰ)根据题意写出数列的前四项是2,8,32,128.;(ⅱ)根据题意写出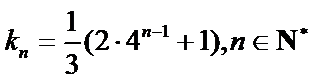
在证明“以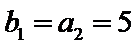
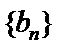
易错点
由题归纳法得数列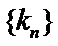
已知






22.求数列

23.设






正确答案
(1)
解析
(1)因为

所以



所以
考查方向
解题思路
1.第(1)问根据等差数列、等比数列的基本量求出通项公式;2.根据第(1)问求出
易错点
1.不会将


正确答案
(1)
解析
(2)

所以

(或
因为



所以,不存在正整数

考查方向
解题思路
1.第(1)问根据等差数列、等比数列的基本量求出通项公式;2.根据第(1)问求出
易错点
1.不会将


已知数列






22.分别求数列

23.若



正确答案
(1)

解析
(Ⅰ)


又因为

设等比数列

由已知

解得


所以,
考查方向
解题思路
先利用已知数列的前n项和求通项公式求出

易错点
1.不会利用数列的前n项和求通项公式;2.对于数列
正确答案
(2)
解析
(Ⅱ)
设数列





当
当


则

1-2得
所以
所以,
考查方向
解题思路
先由第(1)问得到
易错点
1.不会利用数列的前n项和求通项公式;2.对于数列
已知


17.求数列
18.求数列


正确答案
(1)
解析
(1) 设



由


考查方向
解题思路
利用等差数列的性质求出数列
易错点
利用等差数列的性质求通项公式和等比数列的性质混淆;
正确答案
解析
(2)
由
得
① -②得

又
当


考查方向
解题思路
根据公式构造等式求出
易错点
先构造等式做差后求出
扫码查看完整答案与解析