- 二次函数的应用
- 共461题
20.如图所示,某旅游景点有一座风景秀丽的山峰,山上有一条笔直的山路BC和一条索道AC,小王和小李打算不坐索道,而是花2个小时的时间进行徒步攀登。已知



正确答案
由

由正弦定理得
所以,
在
由余弦定理得:
即
即
解得

由于
解析
解析已在路上飞奔,马上就到!
知识点
17.设复数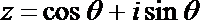
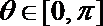
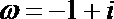

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.解关于

正确答案
∵ 
∴ 

∴ 
∴不等式的解集为
解析
解析已在路上飞奔,马上就到!
知识点
5.若复数z1=3–i,z2=7+2i,(i为虚数单位),则|z2–z1|=( )。
正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
22.函数f(x)=
(1)求a.b的值;
(2)是否存在实常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立?为什么?
(3)在直角坐标系中,求定点A(–3,1)到此函数图象上任意一点P的距离|AP|的最小值。
正确答案
(1)由f(2)=1得2a+b=2,又x=0一定是方程
所以
若无解,则ax+b=1无解,得a=0,矛盾,
若有解为0,则b=1,所以a=
(2)f(x)=
设存在常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,
取x=0,则f(0)+f(m–0)=4,即
又m= –4时,f(x)+f(–4–x)=
所以存在常数m= –4,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,
(3)|AP|2=(x+3)2+(
则|AP|2=(t+1)2+(






=( t–



解析
解析已在路上飞奔,马上就到!
知识点
1.若
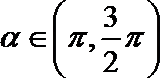
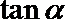
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
(2012•六盘水)如图是教师每天在黑板上书写用的粉笔,它的主视图是( )
正确答案
解析
首先判断该几何体是圆台,然后确定从正面看到的图形即可.
该几何体是圆台,主视图是等腰梯形.
故选C.
本题考查了简单几何体的三视图,属于基础题,比较简单.
知识点
(2012•六盘水)下列命题为真命题的是( )
正确答案
解析
利用确定圆的条件、不等式的性质及多边形的内角与外角等知识进行判断找到正确的即可.
A、平面内不在同一直线上的三点确定一个圆,故本答案错误;
B、五边形的内角和为(5﹣2)×180°=540°,故本选项正确;
C、当c=0时,原式不成立,故本答案错误;
D、两直线平行,同位角相等,故本答案错误.
故选B.
本题考查了确定圆的条件、不等式的性质及多边形的内角与外角等知识,属于基础题,知识点比较多.
知识点
2.函数
正确答案
π
解析
解析已在路上飞奔,马上就到!
知识点
6.ΔABC中,若∠B=30o,AB=2

正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析








