二次函数的应用
共461题

· 二次函数的应用

二次函数的应用
共461题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

7.已知三棱锥的三视图如图所示，则它的外接球表面积为（）

A16

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：填空题

填空题 · 5 分

15. 在中，是边中点，角，，的对边分别是，，，若，则的形状为__________。

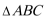
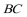
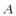
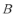
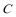
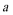
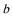
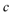
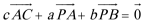
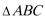
正确答案

等边三角形

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：填空题

填空题 · 4 分

12.在总体中抽取了一个样本，为了便于计算，将样本中的每个数据除以后进行分析，得出新样本的方差为，则估计总体的标准差为（）

正确答案

300

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：单选题

单选题 · 5 分

6．等差数列前n项和为，已知，则（）

A125

B85

C45

D35

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：单选题

单选题 · 5 分

2．设向量，，则是”的（）

A充分但不必要条件

B必要但不充分条件

C充要条件

D既不充分也不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：单选题

单选题 · 5 分

10．设函数在（，+）内有定义．对于给定的正数K，定义函数令=，若对任意的，恒有=，则（）

AK的最大值为2

BK的最小值为2

CK的最大值为1

DK的最小值为1

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：简答题

简答题 · 14 分

19.已知函数，为函数的导函数．

（1）设函数的图象与轴交点为曲线在点处的切线方程是，求的值；

（2）若函数，求函数的单调区间．

正确答案

（1）∵，∴．

∵在处切线方程为，∴，

即，.

（2）．

①当时，，

的单调递增区间为，单调递减区间为．

②当时，令，得或

（ⅰ）当，即时，

的单调递增区间为，单调递减区间为，；

（ⅱ）当，即时，，

故在单调递减；

（ⅲ）当，即时，

在上单调递增，在，上单调递综上所述，当时，的单调递增区间为，单调递减区间为；

当时，的单调递增区间为，单调递减区间为，

当时，的单调递减区间为；

当时，的单调递增区间为，单调递减区间为，．

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：单选题

单选题 · 3 分

12．函数在下列哪个区间是减函数（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：简答题

简答题 · 15 分

22．已知函数，,．

（1）求函数的极大值点与极小值点；

（2）若函数在上有零点，求的最大值（为自然对数的底数）；

（3）设（），试问数列中是否存在相等的两项？若存在，求出所有相等的两项；若不存在，请说明理由。

正确答案

（1）由题知：的定义域为（0,+∞）

∵

∴函数的单调递增区间为　,的单调递减区间为，

所以为的极大值点，为的极小值点．

（2）∵在∈上的最小值为

且=

∴在∈上没有零点，

∴函数在上有零点，并考虑到在单调递增且在单调递减，

故只须且即可，易验证

，

当≤-2且∈Z时均有，所以函数在上有零点，

即函数在上有零点,∴的最大值为-2．

（3）利用导数易证，当时, 所以．因为，所以

令，得：，结合得：

因此，当时，有，

所以当时，，即：，

又通过比较、、、的大小知：，

因为，且时，

所以若数列中存在相等的两项，只能是、与后面的项可能相等，

又，，所以数列中存在唯一相等的两项，

即：．

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：单选题

单选题 · 5 分

5. 如图，设是图中边长为的正方形区域，是内函数图象下方的点构成的区域。在中随机取一点，则该点在中的概率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

继续学习学习下一知识点

下一知识点 : 幂函数的概念、解析式、定义域、值域

百度题库 > 高考 > 理科数学 > 二次函数的应用

扫码查看完整答案与解析