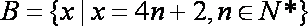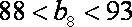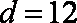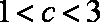- 二次函数的应用
- 共461题
已知直线l:Ax+By+C=0(A2+B2≠0),两点Pl(xl,yl),P2(x2,y2)满足
,记m=
正确答案
解析
略
知识点
在直角坐标系中,点O为坐标原点,已知




正确答案

解析
略
知识点
已知函数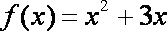
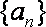
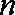
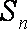
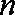
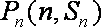
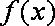
(1)求数列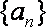
(2)设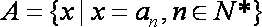
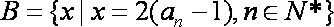
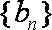
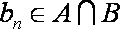
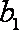

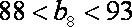
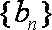
(3)设数列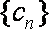
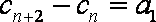
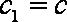
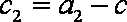
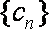
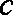
正确答案
见解析
解析
(1)∵点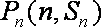
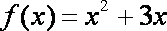
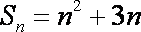
当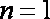
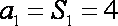
当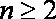
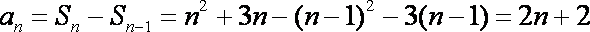
当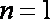
故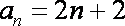
(2)∵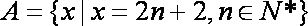
∴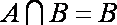
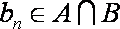
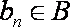
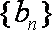
又
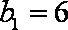
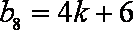
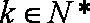
又∵
∴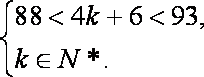

设等差数列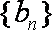
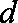
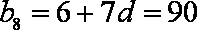
故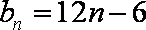
(3) 由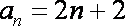
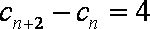
即数列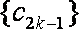
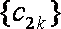
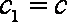
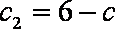
所以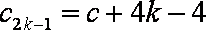
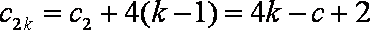
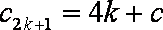
∵数列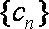
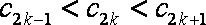
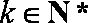
∴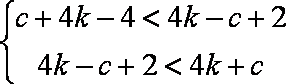
∴实数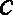
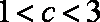
知识点
函数






(1)指出函数


(2)试研究对数函数



(3)若




正确答案
(1)对等函数(2)当





解析
解析:(1)

(2)研究对数函数







当



当



总之,当





(3)对任意


1)若

2)若





3)以下均在
当

当










综上讨论,当


若当









若


综上讨论,若当





知识点
设P是函数


正确答案
解析


故
知识点
数列


(1)当


(2)当




(3)设数列


正确答案
见解析
解析
(1)

设等比数列





(2)证明:




(3)

数列


当


当


知识点
已知




正确答案
见解析。
解析



知识点
若函数f(x)=2sin(ωx+φ),x∈R(其中ω>0,

正确答案
解析
解:由

∵
知识点
若x,y满足

正确答案
-2
解析
因为底数




知识点
在斜三角形
(1)若

(2)若

正确答案
见解析
解析
解:(1)由正弦定理,得
从而

由余弦定理,得
整理得

(2)在斜三角形

所以

即
故
整理,得
因为△ABC是斜三角形,所以sinAcosAcosC
所以
知识点
扫码查看完整答案与解析