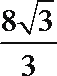二次函数的应用
共461题

· 二次函数的应用

二次函数的应用
共461题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

3．已知函数在处的导数为，则实数的值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：单选题

单选题 · 5 分

7．已知，，且是的必要不充分条件，则的取值范围为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：简答题

简答题 · 14 分

16.设定义在上的函数的最小正周期为。

（1）若，，求的最大值；

（2）若，，求的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：简答题

简答题 · 16 分

18.如图，某兴趣小组测得菱形养殖区的固定投食点到两条平行河岸线的距离分别为4m、8m，河岸线与该养殖区的最近点的距离为1m，与该养殖区的最近点的距离为2m。

（1）如图甲，养殖区在投食点的右侧，若该小组测得，请据此算出养殖区的面积；

（2）如图乙，养殖区在投食点的两侧，试在该小组未测得的大小的情况下，估算出养殖区的最小面积。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：简答题

简答题 · 16 分

18.如图中，AB=AC=，BC=2，以B、C为焦点的椭圆恰好过AC的中点P 。

（1）求椭圆的标准方程；

（2）过椭圆的右顶点做直线l与圆相交于M,N两点，试探究点M,N能将圆E分割成弧长比值为1:3的两段弧吗？若能，求出直线l的方程；若不能，请说明理由。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：简答题

简答题 · 14 分

22．已知函数。

（1）求的单调区间；

（2）若对，，都有，求的取值范围。

正确答案

（1），

令得

当时，

在和上递增，在上递减；

当时，

在和上递减，在上递增

（2）当时，；

所以不可能对，都有；

当时有（1）知在上的最大值为，

所以对，

都有

即，

故对，都有时，

的取值范围为。

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：单选题

单选题 · 5 分

8．函数处的切线方程是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：填空题

填空题 · 5 分

7．设△ABC的内角A，B，C的对边分别为a，b，c，且a=1，b=2，cosC=，则sinB=（）

正确答案

解析

∵C为三角形的内角，cosC=，

∴sinC==，

又a=1，b=2，

∴由余弦定理c2=a2+b2﹣2abcosC得：c2=1+4﹣1=4，

解得：c=2，

又sinC=，c=2，b=2，

∴由正弦定理=得：sinB===．

故答案为：

知识点

二次函数的应用

题型：填空题

填空题 · 5 分

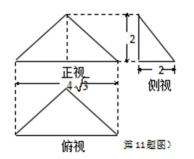
11．已知某几何体的三视图如图所示，则该几何体的体积是___________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：简答题

简答题 · 10 分

23．设是给定的正整数，有序数组同时满足下列条件：

① ,；

②对任意的,都有．

（1）记为满足“对任意的，都有”的有序数组的个数，求；

（2）记为满足“存在，使得”的有序数组的个数，求。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

继续学习学习下一知识点

下一知识点 : 幂函数的概念、解析式、定义域、值域

百度题库 > 高考 > 理科数学 > 二次函数的应用

扫码查看完整答案与解析