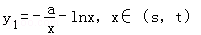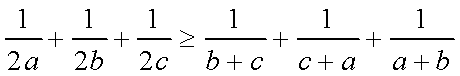- 二次函数的应用
- 共461题
已知函数


正确答案
见解析
解析
证明:由

令

当



当x>0时,


所以

故

所以函数

则

知识点
已知在平面直角坐标系



正确答案
解析
圆C方程为


知识点
已知函数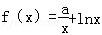
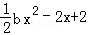
(1)求函数f(x)的单调区间;
(2)记函数h(x)=f(x)+g(x),当a=0时,h(x)在(0,1)上有且只有一个极值点,求实数b的取值范围;
(3)记函数F(x)=|f(x)|,证明:存在一条过原点的直线l与y=F(x)的图象有两个切点。
正确答案
见解析
解析
(1)因为f'(x)=﹣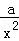
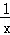
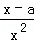
①若a≤0,则f'(x)>0,f(x)在(0,+∞)上为增函数,
②若a>0,令f'(x)=0,得x=a,
当0<x<a时,f'(x)<0;当x>a时,f'(x)>0。
所以(0,a)为单调减区间,(a,+∞)为单调增区间。
综上可得,当a≤0时,函数f(x)在(0,+∞)上为增函数,
当a>0时,函数f(x)的单调减区间为(0,a),单调增区间为(a,+∞),
(2)a=0时,h(x)=f(x)+g(x)=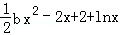
∴h'(x)=bx﹣2+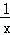
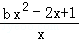
h(x)在(0,1)上有且只有一个极值点,即h'(x)=0在(0,1)上有且只有一个根且不为重根,
由h'(x)=0得bx2﹣2x+1=0,…(6分)
( i)b=0,x=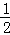
( ii)b>0时,b•12﹣2•1+1<0,即0<b<1;
( iii)b<0时,b•12﹣2•1+1<0,得b<1,故b<0;
综上所述,得:h(x)在(0,1)上有且只有一个极值点时,b<1.
(3)证明:由(1)可知:
( i)若a≤0,则f'(x)≥0,f(x)在(0,+∞)上为单调增函数,
所以直线l与y=F(x)的图象不可能有两个切点,不合题意
(ⅱ)若a>0,f(x)在x=a处取得极值f(a)=1+lna。
若1+lna≥0,a≥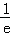
故0<a<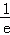
则直线l与y=F(x)的图象有两个切点即为直线l与
和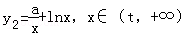
y1'=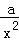
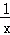
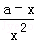
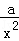
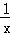

设切点分别为A(x1,y1),B(x2,y2),则0<x1<x2,且


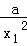
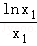
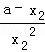
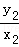
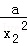
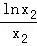
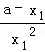
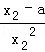
即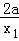
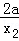
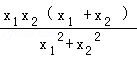
①﹣②得: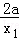
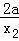
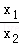
由③中的a代入上式可得:(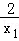
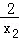
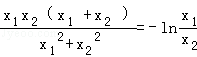
即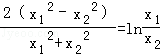
令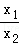
因为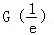
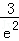
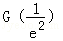
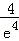
故存在k0∈(0,1),使得G(k0)=0,
即存在一条过原点的直线l与y=F(x)的图象有两个切点,
知识点
已知抛物线





正确答案
解析
将

知识点
定义:

正确答案
解析
易得


知识点
已知f(x)=log2(x﹣1),若实数m,n满足f(m)+f(n)=2,则mn的最小值是 。
正确答案
9
解析
由f(x)=log2(x﹣1),且实数m,n满足f(m)+f(n)=2,
所以log2(m﹣1)+log2(n﹣1)=2。
则
由①得(m﹣1)(n﹣1)=4,即mn﹣(m+n)=3。
所以3=mn﹣(m+n)
即


因为m>1,n>1.所以
知识点
在△ABC中,若

正确答案

解析
设




求得

知识点
设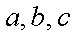
正确答案
见解析
解析
因为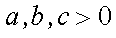
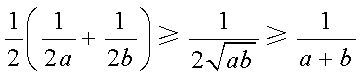
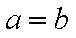
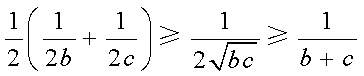
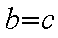
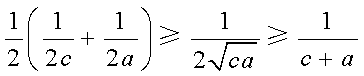
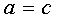
三个不等式相加得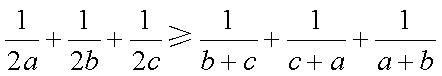
当且仅当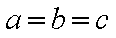
知识点
定义在R上的函数




正确答案
解析
∵定义在R上的函数f(x)满足f(0)=0,f(x)+f(1−x)=1,








知识点
设数列




(1)求数列
(2)若

正确答案
(1)
(2)
解析
(1)因为点


当

两式相减得

又当

所以数列



(2)由(1)知,
记数列



两式相减得
所以数列

知识点
扫码查看完整答案与解析