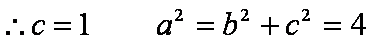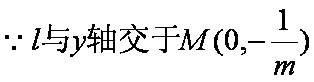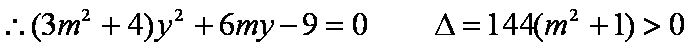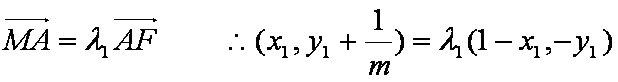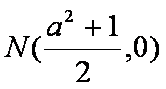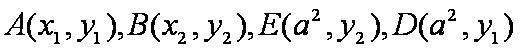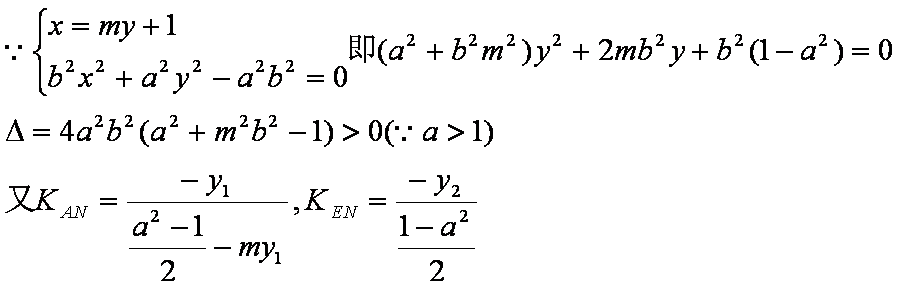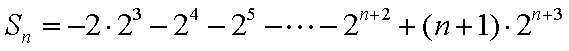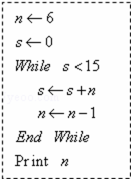- 二次函数的应用
- 共461题
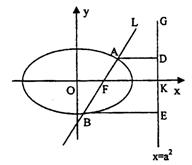
如图,已知直线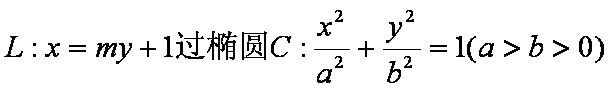
(1)已知抛物线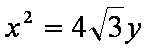
①求椭圆C的方程;
②若直线L交y轴于点M,且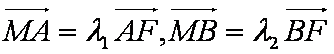

(2)连接AE,BD,试探索当m变化时,直线AE、BD是否相交于一定点N?若交于定点N,请求出N点的坐标并给予证明;否则说明理由.
正确答案
见解析
解析
解析:(1)易知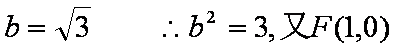

设
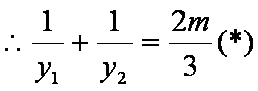
又由

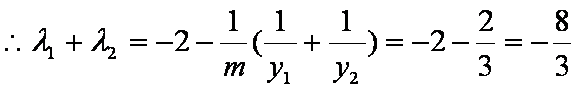
(2)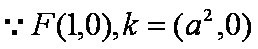
猜想:当m变化时,AE与BD相交于定点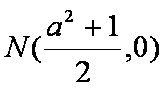
证明:设
当m变化时首先AE过定点N
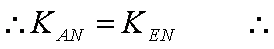
同理可得B、N、D三点共线
∴AE与BD相交于定点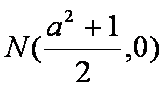
知识点
在平面直角坐标系








(1)求函数
(2)设






正确答案
(1)
解析
解析:
(1)由题意,得

所以
因为


(2)因为


在

即

知识点
已知函数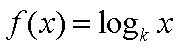
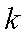
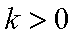
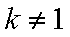
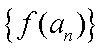
数列.
(1)求证:数列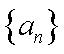
(2) 若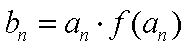
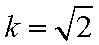
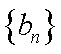
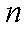
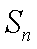
正确答案
见解析
解析
解析:(1) 证:由题意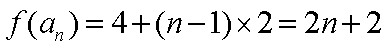
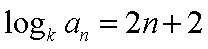
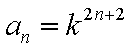
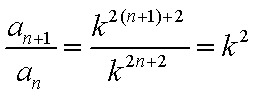
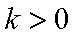
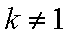
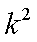
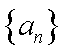
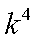
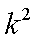
(2)由(1)知,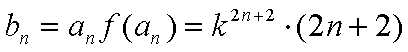
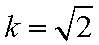
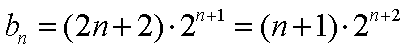
∴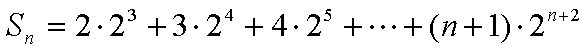
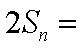
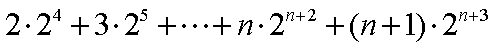
②-①,得
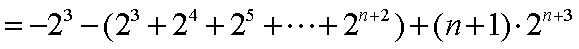
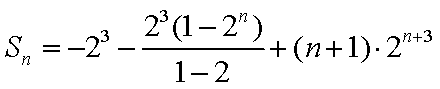
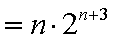
(3)由(1)知,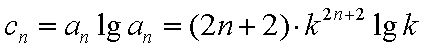
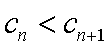
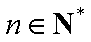
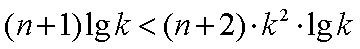
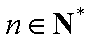
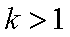
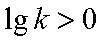
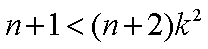
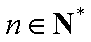
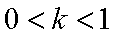
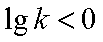
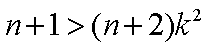
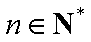
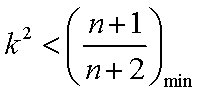
∵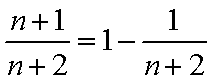
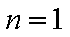
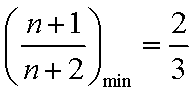
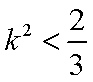
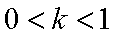
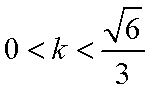
综上所述,存在实数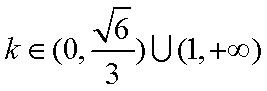
知识点
某射击小组有甲、乙两名射手,甲的命中率为
(1)若
(2)计划在2011年每月进行1次检测,设这12次检测中该小组获得“先进和谐组”的次数ξ,如果Eξ≥5,求P2的取值范围。
正确答案
见解析
解析
(1)∵

根据“先进和谐组”的定义可得
该小组在一次检测中荣获“先进和谐组”的包括两人两次都射中,两人恰好各射中一次,
∴该小组在一次检测中荣获“先进和谐组”的概率
P=(C21•



(2)该小组在一次检测中荣获先进和谐组”的概率
P=(C21•

而ξ~B(12,P),所以Eξ=12P
由Eξ≥5知,(
解得:
知识点
已知函数
则
正确答案
解析
根据图像







函数的最小正周期是



知识点
已知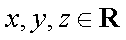
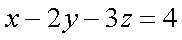
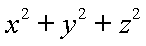
正确答案
见解析。
解析
由柯西不等式,得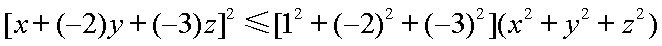
即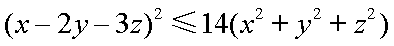
即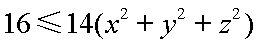
所以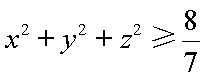
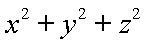
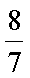
知识点
某校有高级教师26人,中级教师104人,其他教师若干人,为了了解该校教师的工资收入情况,若按分层抽样从该校的所有教师中抽取56人进行调查,已知从其他教师中共抽取了16人,则该校共有教师 人。
正确答案
182
解析
设该校其他教师有


知识点
设
其中
正确答案
492
解析
两边求导,有:

再对上式求导,有


知识点
如图所示是一算法的伪代码,执行此算法时,输出的结果是 。
正确答案
3
解析
根据题中的程序框图,可得
该程序经过第一次循环,因为s=0<15,所以得到新的S=0+6=6,n=5;
然后经过第二次循环,因为s=6<15,所以得到新的S=6+5=11,n=4;
然后经过第三次循环,因为s=11<15,所以得到新的S=11+4=15,n=3;
接下来判断:因为s=15,不满足s<15,所以结束循环体并输出最后的n,
综上所述,可得最后输出的结果是3
故答案为:3
知识点
已知




正确答案
解析
设线段BC的中点为D,则

∴
∴

∴


即动点

知识点
扫码查看完整答案与解析