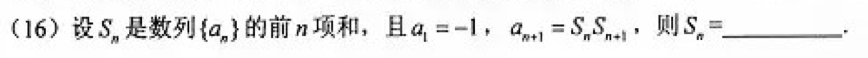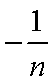由an与Sn的关系求通项an
共102题

· 由an与Sn的关系求通项an

由an与Sn的关系求通项an
共102题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

正确答案

ＬＵＥ

知识点

由an与Sn的关系求通项an其它方法求和

题型：简答题

简答题 · 16 分

19. 设数列的前项和，，，且当时，．

（1）求证:数列是等比数列，并求数列的通项公式；

（2）令，记数列的前项和为．设是整数，问是否存在正整数，使等式成立？若存在，求出和相应的值；若不存在，说明理由．

正确答案

见解析

解析

解：（1）当时, ,,

代入并化简得,

而恒为正值,∴

∴数列是等比数列.

∴.当时,,

又，∴

（2）当时，,此时，又

∴.

故，

当时，

，

若，

则等式为，不是整数，不符合题意；

若，则等式为，

∵是整数, ∴必是的因数, ∵时

∴当且仅当时，是整数，从而是整数符合题意.

综上可知，当时，存在正整数，使等式成立，

当时，不存在正整数使等式成立.

考查方向

本题考查了等比数列的证明及数列的通项公式求法

解题思路

利用，得数列是等比数列.

易错点

忽略n的范围的讨论。

知识点

由an与Sn的关系求通项an等比数列的判断与证明数列与函数的综合数列与不等式的综合

题型：填空题

填空题 · 5 分

16.设是数列的前n项和，且，，则________.

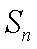
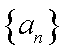
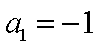
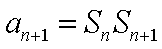
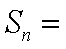
正确答案

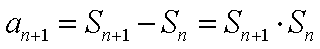
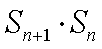
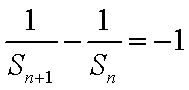
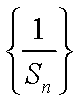
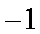
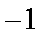
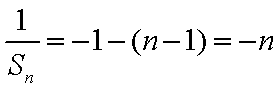
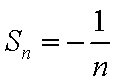
试题分析：由已知得，两边同时除以，得，故数列是以为首项，为公差的等差数列，则，所以.

解析

解析已在路上飞奔，马上就到！

知识点

由an与Sn的关系求通项an其它方法求和

题型：单选题

单选题 · 5 分

已知集合，，则＝（）

正确答案

解析

略

考查方向

集合

解题思路

集合

知识点

由an与Sn的关系求通项an

题型：填空题

填空题 · 5 分

11. 已知数列是首项为1，公差为的等差数列，前项和为，设

，若数列是递减数列，则实数的取值范围是

正确答案

解析

，所以，因为数列是递减数列，所以，所以，化为：，令，，即可得出时只需且，即。则实数的取值范围是。

考查方向

①等差数列求和②递减数列③恒成立。

解题思路

利用求和公式可得。可得，由数列是递减数列，所以，即可得出。

易错点

①计算能力②递减数列的应用③注意恒成立问题。

知识点

由an与Sn的关系求通项an等差数列的性质及应用数列与不等式的综合

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 由递推关系式求数列的通项公式

百度题库 > 高考 > 理科数学 > 由an与Sn的关系求通项an

扫码查看完整答案与解析