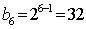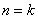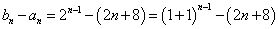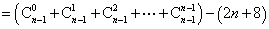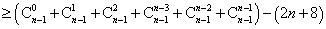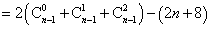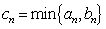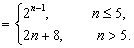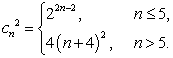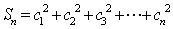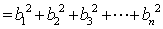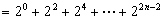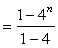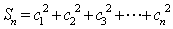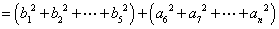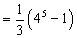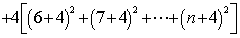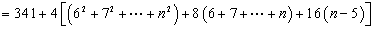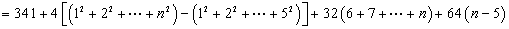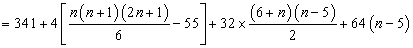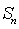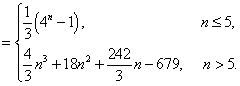- 由an与Sn的关系求通项an
- 共102题
1
题型:填空题
|
已知等差数列




正确答案
20
解析
略
知识点
由an与Sn的关系求通项an
1
题型:简答题
|
设等比数列




(1)求数列
(2)在




求证:

正确答案
见解析。
解析
(1)设等比数列






即

当


即
(2)①

设

① -②得:
=
知识点
由an与Sn的关系求通项an等差数列的性质及应用数列与不等式的综合
1
题型:
单选题
|
设等差数列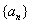
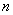
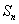
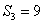
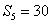

正确答案
D
解析
略
知识点
由an与Sn的关系求通项an
1
题型:简答题
|
已知等差数列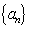
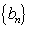
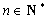
(1)求数列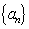
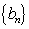
(2)设第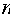
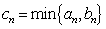
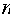
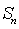
(注: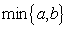

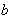
正确答案
见解析。
解析
(1)因为等差数列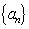
所以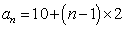
即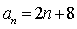
因为等比数列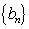
所以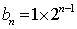
即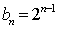
(2)因为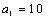
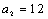
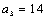
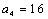
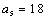
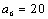
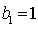
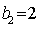
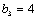
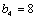
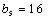
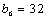
易知当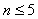
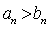
下面证明当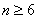
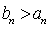
方法1:①当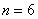
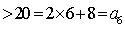
②假设当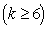
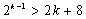
则有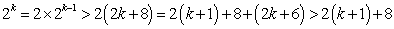
这说明当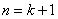
综合①②可知,不等式对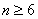
所以当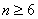
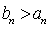
方法2:因为当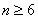
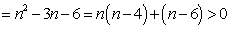
所以当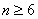

所以
则
当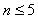
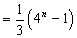
当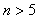
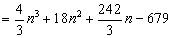
综上可知,
知识点
由an与Sn的关系求通项an
1
题型:简答题
|
阅读:
应用上述解法,求解下列问题:
(1)已知


(2)已知

(3)已知正数



求证:
正确答案
见解析
解析
(1)
而
当且仅当



(2)
而

当且仅当


所以函数

(3)
当且仅当

知识点
由an与Sn的关系求通项an
下一知识点 : 由递推关系式求数列的通项公式
扫码查看完整答案与解析