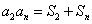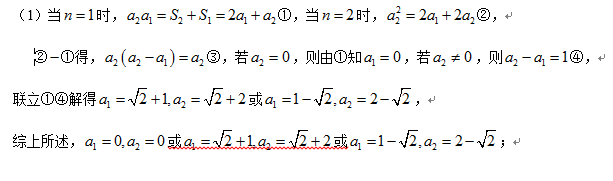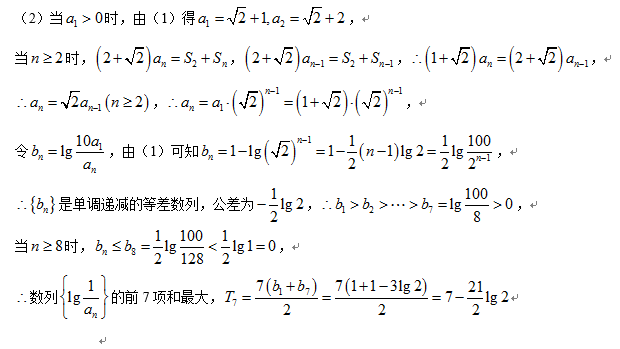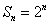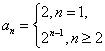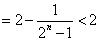- 由an与Sn的关系求通项an
- 共102题
设数列












正确答案
见解析。
解析
(1)当



(2)当
所以


所以数列


(3)当




所以
知识点
设









(1)若

(2)是否存在数列
(3)是否存在数列

正确答案
见解析
解析
(1)由题意,创新数列为3,5,5,5,5的所有数列
3,5,1,2,4;……………2分
3,5,1,4,2;
3,5,2,1,4;
3,5,2,4,1;
3,5,4,1,2;
3,5,4,2,1;………………4分
(2)
知识点
已知各项为正的数列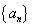
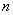
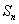
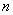
(1)求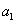
(2)求数列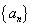
(3)若数列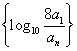
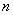
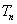
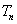
正确答案
见解析。
解析
解:
知识点
已知数列



正确答案
解析
略
知识点
已知数列



(1)求数列

(2)设


(3)设

正确答案
见解析。
解析
(1)由题意,当

两式相减得

由

所以对一切正整数n,有
故

(2)由(1),得
所以
①两边同乘以

①-②,得
所以
故
(3)由(1),得

知识点
从





(1)当

(2)求
(3)求证:
正确答案
见解析
解析
(1)符合要求的递增等差数列为1,2,3;2,3,4;3,4,5;1,3,5,共4个.
所以
(2)设满足条件的一个等差数列首项为






对于给定的












所以当


(3)设等差数列首项为



记





对于给定的




所以当

易证
又因为

所以
所以

即
知识点
已知数列



(1)求数列{an}的通项公式;
(2)令






正确答案
见解析。
解析
知识点
已知数列
(1)
(2)数列
正确答案
见解析。
解析
知识点
已知数列



(1)设

(2)在数列
(3)若





正确答案
见解析
解析
(1)将已知条件
当


------------------3分
所以数列


-----------------4分
(2)由(1)知


-----------------1分
假设在数列






将


式得
化简得,


所以,存在满足条件的连续三项为


(3)若




得
------------------2分
由于若




① 若




② 若



③ 若




舍去;
④ 若




综上①②③④可知,只有当




时满足条件点列


------------------5分
知识点
正项数列
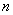

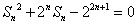
(1)求数列
(2)令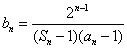
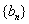
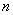
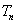
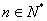
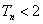
正确答案
见解析
解析
(1)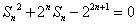
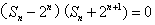
当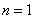
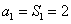
当
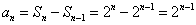
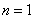
(2)当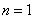
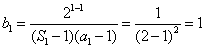
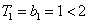
当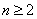
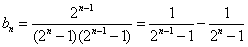
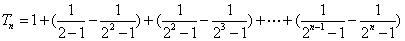
综上,对于任意的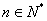
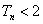
知识点
扫码查看完整答案与解析