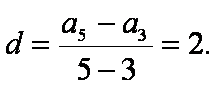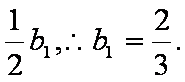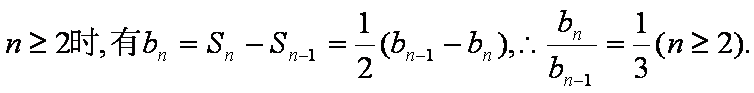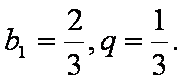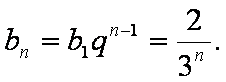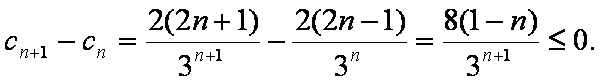- 由an与Sn的关系求通项an
- 共102题
若数列{an}的前n项和为 ,则下列命题:
(1)若数列{an}是递增数列,则数列{Sn}也是递增数列;
(2)数列{Sn}是递增数列的充要条件是数列{an}的各项均为正数;
(3)若{an}是等差数列(公差d

(4)若{an}是等比数列,则
其中,正确命题的个数是
正确答案
解析
数列{an}的前n项和为Sn,故 Sn =a1+a2+a3+…+an.若数列{an}是递增数列,则数列{Sn}不一定是递增数列,如当an<0 时,数列{Sn}是递减数列,故(1)不正确;由数列{Sn}是递增数列,不能推出数列{an}的各项均为正数,如数列:0,1,2,3,…,满足{Sn}是递增数列,但不满足数列{an}的各项均为正数,故(2)不正确;若{an}是等差数列(公差d≠0),则由S1•S2…Sk=0,不能推出a1•a2…ak=0,例如数列:-3,-1,1,3,满足S4=0,但 a1•a2•a3•a4≠0,故(3)不正确,若{an}是等比数列,则由S1•S2…Sk=0(k≥2,k∈N)可得数列的{an}公比为-1,故有an+an+1=0.由an+an+1=0可得数列的{an}公比为-1,可得S1•S2…Sk=0(k≥2,k∈N),故(4)正确,故选B。
知识点
已知等差数列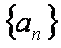
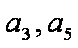
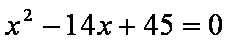
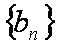
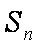

(1)求数列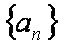
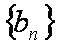
(2)记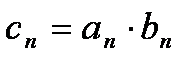
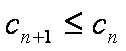
正确答案
见解析
解析
解:(1)∵a3,a5是方程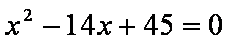
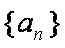
∴a3=5,a5=9,公差
∴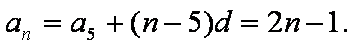
又当n=1时,有b1=S1=1-
当
∴数列{bn}是等比数列,
∴
(2)由(1)知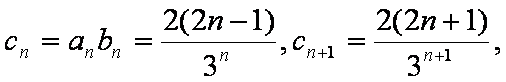
∴
∴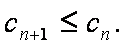
知识点
已知数列



(1)求数列
(2)设




正确答案
见解析。
解析
(1)由题设知
由

所以
可见,数列

所以
(2)

=
知识点
已知各项均为正数的数列



(1)求数列
(2)若



正确答案
见解析
解析
(1)由题意知
当

当
两式相减得
整理得:
∴数列

(2)
∴


①-②得

知识点
17.已知Sn为数列{an}的前n项和,且2an=Sn+n.
(1)若bn=an+1,证明:数列{bn}是等比数列;
(2)求数列{Sn}的前n项和Tn。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析