- 二项式定理
- 共260题
13. 如果

正确答案
-2
解析




考查方向
解题思路
利用定积分求n=4,再求二项展开式的指定项或指定项的系数
易错点
不会求定积分的值,不会求二项展开式的指定项或指定项的系数。
知识点
12.在二项式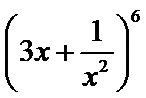
正确答案
1215
解析
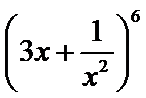
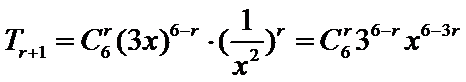
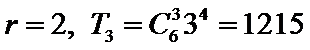
考查方向
解题思路
写出二项展开式,确定r,直接计算
易错点
本题易错在二项展开式记忆错误
知识点
10. 在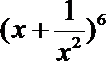
正确答案
15
解析
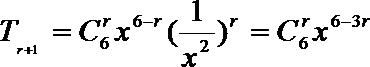
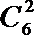
考查方向
本题主要考察了二项式定理中的指定项的问题,属于中档题,是高考的热点,解决此类题的关键:用二项式定理中的通项,让x的次数为0。
易错点
本题易在用二项式定理中的通项时发生错误,导致题目无法进行。
知识点
14.
正确答案
解析
由题设知:
考查方向
本题主要考查了二项式展开式及二项式系数的概念。
易错点
本题必须注意二项式系数与系数的区别,还有就是题目要求写出此项,忽视则会出现错误。
知识点
9.


正确答案
解析
由题意知








考查方向
本题考查了二项式定理.
解题思路
先由二项式系数之和求


易错点
混淆二项式系数与系数.
知识点
若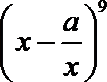
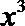
正确答案
1
解析
根据二项式的展开式,可得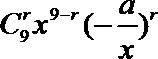
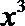
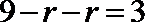
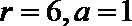
考查方向
本题主要考查了二项式系数的概念以及二项式展开的运算能力
易错点
容易混淆二项式系数与项的系数的概念
知识点
11.二项式
正确答案
20
解析




考查方向
解题思路
写出二项展开式,确定r,直接计算
易错点
本题易错在二项展开式记忆错误
知识点
11.在
正确答案
﹣90
解析
考查方向
解题思路
先写出通项再根据题意确定r的值,再找出含x3的项的系数即可。
易错点
1、本题易在书写通项时在“-”号上出错 。
知识点
13.二项式

正确答案
60
解析
由题可知,Tk+1=C6k(x)6-k-k(-2)k=60x2,可求得系数为60。
考查方向
本题主要考查了二项式定理。
解题思路
解题步骤如下:利用通项公式求解。
易错点
本题要注意通项公式。
知识点
7.

正确答案
解析
由题可知,原式=(x2+2x+1)(x-2)4,则含x3项为
考查方向
本题主要考查二项式定理
解题思路
1、求出x3项;
2、利用通项公式求解,即可得到结果。
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在求x3项时发生错误。
知识点
扫码查看完整答案与解析









