- 二项式定理
- 共260题
10.在

正确答案
60
知识点
设i为虚数单位,则
正确答案
知识点
8. 在

正确答案
解析

通项
取
常数项为
知识点
2.设i为虚数单位,则
正确答案
解析
二项式


考查方向
解题思路
本题考查二项式定理及复数的运算,复数的概念及运算也是高考的热点,几乎是每年必考内容




易错点
本题考查二项式定理及复数的运算,在用二项式的通项时,易把r+1项看成r项
知识点
8.在报名的


正确答案
120
解析
由题意得,去掉选5名女教师情况即可:
考查方向
解题思路
涉及排列与组合问题,区分的关键是看选出的元素是否与顺序有关,排列问题与顺序有关,组合问题与顺序无关.“含”与“不含”的问题:“含”,则先将这些元素取出,再由另外元素补足;“不含”,则先将这些元素剔除,再从剩下的元素中去选取.通常用直接法分类复杂时,考虑逆向思维,用间接法处理.
易错点
本题方法较多需要灵活运用
知识点
10.

正确答案
解析

考查方向
解题思路
求特定项系数问题可以分两步完成:第一步是根据所给出的条件(特定项)和通项公式,建立方程来确定指数(求解时要注意二项式系数中n和r的隐含条件,即n,r均为非负整数,且n≥r);第二

易错点
不能准确记忆二项式定理的通项公式导致出错。
知识点
12.若(ax2+
正确答案
-2
知识点
11. 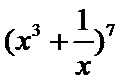
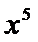
正确答案
解析
由题意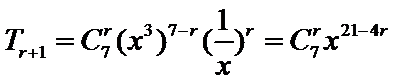

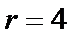
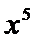
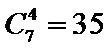
考查方向
解题思路
先利用公式展开,然后找到次数为5的项,进而求出系数。
易错点
二项式展开式公式记忆混淆,找系数时次数有遗漏项
知识点
13. 二项式




正确答案
解析
∵二项式

∴
考查方向
解题思路
利用二项展开式的系数求出
易错点
本题必须注意二项式系数和项的系数弄混淆
知识点
14.
正确答案
解析


故常数项为
考查方向
解题思路
1.先写出
2. 令
易错点
1.展开式中的通项公式易丢掉-1导致出错;
2.对于通项公式的化简即指数幂的运算出错,
知识点
扫码查看完整答案与解析