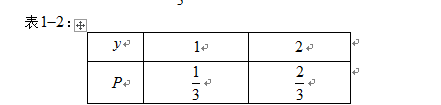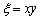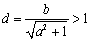- 二项式定理
- 共260题
在



正确答案
解析
令





知识点
已知锐角








(1)求角
(2)设函数



正确答案
(1)
解析
(1)因为
所以


所以

(2)
由已知
因为



所以

知识点
给出下列命题:
(1)已知事件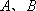
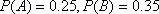
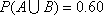
(2)已知事件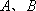
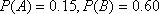
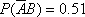
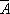
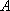
(3)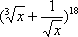
则其中真命题的序号是 [答]( )。
正确答案
解析
略
知识点
现有一枚质地均匀的骰子,连续掷两次,所掷的点数依次记为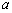
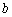
(1)若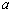
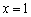
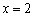
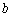
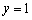
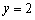
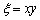
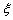
(2)设命题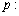
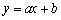
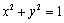
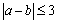
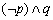
正确答案
见解析。
解析
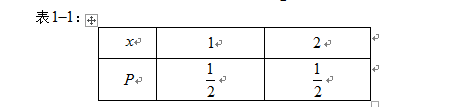
(1)易知事件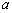
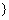
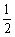
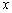
事件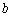
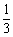
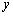
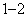
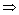
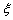
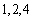
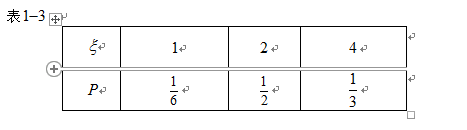
由上述二表可知: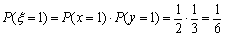
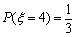
于是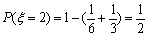
从而可知随机变量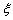
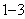
进而可知随机变量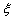
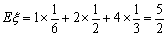
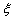
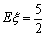
(2)命题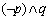
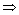
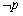
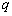
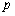
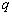
若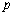
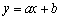
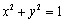
于是直线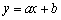
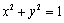
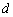
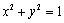
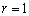
即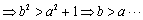
若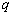
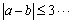
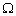
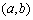
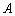
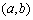
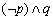
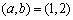
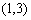
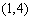
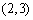
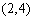

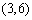
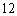
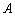
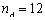
又易知事件

则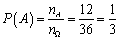
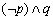
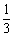
知识点
在

正确答案
1-
解析
略
知识点
在


正确答案
256
解析
略
知识点
二项式(1+sinx)n的展开式中,末尾两项的系数之和为7,且系数最大的一项的值为

正确答案
解析
略。
知识点
已知




正确答案
解析
略
知识点
已知二项式






正确答案
2
解析
略
知识点
若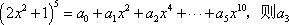
正确答案
80
解析
略
知识点
扫码查看完整答案与解析