- 二项式定理
- 共260题
5.若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.
正确答案
解析
由题可知,T8=C107(2x)3=960x3,可求得T8=
考查方向
本题主要考查了二项式定理。
解题思路
本题考查二项式定理,解题步骤如下:利用通项公式求解。
易错点
本题要注意通项公式。
知识点
13.若(a+x)(1-x)4的展开式的奇次项系数和为48,则实数a之值为____.
正确答案
-5
解析
本题属于二项式定理的问题,题目的难度较小。注意首先将多项式展开。
考查方向
本题主要考查了二项式定理的问题。
易错点
本题必须注意二项式系数的性质,忽视则会出现错误。
知识点
7. 
正确答案
解析

所以常数项为
考查方向
解题思路
第一步,求第二个式子展开式中
易错点
1、常数项的来源有两种,一种是前面因式中的

知识点
14.若


正确答案
2
解析
因为

所以






考查方向
解题思路
根据展开式 求a和b的关系
易错点
展开式公式记错、基本不等式“一正”“二定”“三相等”
知识点
13.
正确答案
-160
解析



考查方向
解题思路
1.先写出

2.然后利用2x,-1分别与


易错点
不理解如何算出错
知识点
4.(x-2y)6的展开式中,x4y2的系数为
正确答案
解析
由

考查方向
解题思路
利用二项展开式的通项公式
易错点
公式掌握不好,或运算失误;混淆系数与二项式系数。
知识点
13.在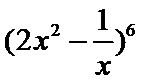
正确答案
60
解析
二项式展开式的通项为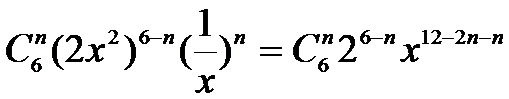
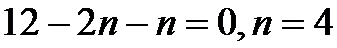
考查方向
解题思路
直接写二项式展开式的通项,然后看哪一项x次数为0
易错点
二项式的展开式的公式记错
知识点
5.在

正确答案
解析
该二次项展开为
即
展开式中
可令
所以
所以


所以选B
考查方向
解题思路
根据二项式展开式,求得
易错点
二项式展开后,忽略某几项乘积为
知识点
11.在

正确答案
解析
因为



知识点
扫码查看完整答案与解析