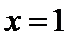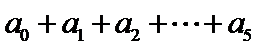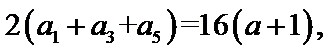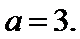- 二项式定理
- 共260题
13.(a+x)(1+x)4的展开式中x的奇数次幂项的系数之和为32,则a=______.
正确答案
3
解析
设
令
得: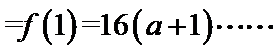
令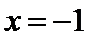
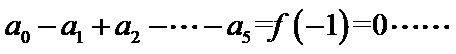
①-②得
所以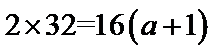
解得
考查方向
解题思路
本题考查了二项式定理的应用,用二项式定理展开,建立方程可算出a的值。
易错点
易在二项式定理展开时易错
知识点
14.已知

正确答案
5
解析
根据二项展开式的通项公式可知








考查方向
解题思路
利用“找伙伴”的办法可知1对

易错点
本题容易对
知识点
15.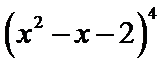
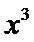
正确答案
-40
解析
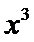
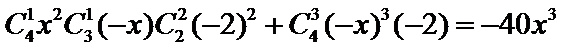
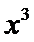
考查方向
解题思路
四个因式相乘,其中一个因式出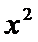
易错点
漏掉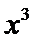
知识点
13.已知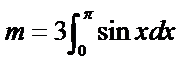
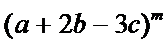
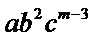
正确答案
-6480
解析
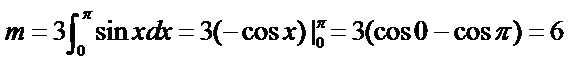
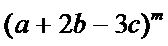
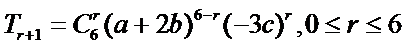
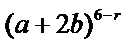
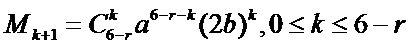
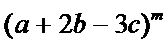
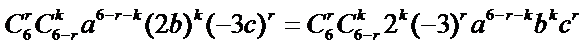
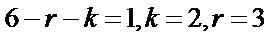
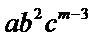
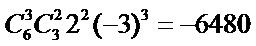
考查方向
解题思路
1.先利用定积分求出m的值;
2.写出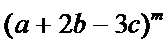
易错点
1. 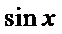
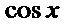
2.对于三项的二项式定理不知道怎么办。
知识点
13.若

正确答案
1
解析
∵

令


依题意,有

故此题答案为1。
考查方向
本题主要考查了二项展开式及二项式中通项的应用,在近几年的各省高考试题中出现的频率较高,常易与函数,不等式,数列等知识点交汇命题,较易。
解题思路
先写出通项再根据题意找出常数项,即就是
易错点
1、本题易在书写通项时出错 。
2、此类题目要教会学生把通项化归成“
知识点
10. 在

正确答案
90
解析
由题可知,

考查方向
解题思路
本题考查二项式定理,解题步骤如下:利用二项式定理的通项公式求解即可
易错点
本题易在求展开式上发生错误。
知识点
14.
正确答案
84
解析
展开式中第

令

所以常数项为
应填84.
考查方向
解题思路
本题主要考查二项式定理,及其展开式的性质,
解题步骤如下:
①写出二项展开式的通项;
②由条件求出常数项即可以。
易错点
本题易记错二项展开式的通项,得出错误答案。
知识点
14.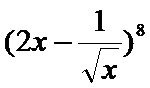
正确答案
1
解析
二次项系数和x的取值无关,所以令x=1,可以得到各项展开后和为1.
考查方向
解题思路
填空题可以选取特殊值
易错点
二项式展开后,逐一计算,繁琐容易出错
知识点
14.已知


正确答案
解析
该二次项展开为






考查方向
解题思路
根据二项式展开式,求得
易错点
二项式展开后,忽略某几项乘积为
知识点
16. 某大学自主招生考试面试环节中,共设置两类考题,A类题有4个不同的小题,B类题有6个不同的小题, 某考生从中任抽取四道题解答.
(Ⅰ)求该考生至少抽取到2道B类题的概率;
(Ⅱ)设所抽取的四道题中B类题的个数为X,求随机变量X的分布列与期望.
正确答案
见解析.
解析
试题分析:本题属于概率统计中的基本问题,题目的难度是逐渐由易到难.
(Ⅰ)设事件A: ” 该考生至少取到2道B类题”.
(2)随机变量X的取值分别为0,1,2,3,4,



∴随机变量X的分布列为:
∴随机变量X的期望为:
考查方向
解题思路
本题考查概率统计,解题步骤如下:1、利用概率公式求解。2、写出基本事件的内容,并求出相应的概率。
易错点
1、第一问中的概率的计算。2、第二问中基本事件对应的概率。
知识点
扫码查看完整答案与解析