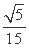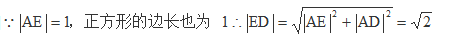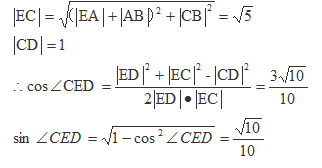- 相似三角形的判定
- 共19题
1
题型:简答题
|
如图,


(1)AC·BD=AD·AB;
(2)AC=AE。
正确答案
见解析
解析
证明:(1)由AC与
同理∠ACB=∠DAB,
所以△ACB∽△DAB。
从而
(2)由AD与
又∠ADE=∠BDA,得△EAD∽△ABD。
从而
结合(1)的结论,AC=AE
知识点
相似三角形的判定相似三角形的性质弦切角
1
题型:
单选题
|
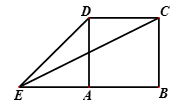
如图,正方形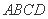
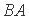
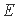
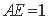
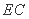
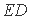
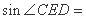
正确答案
B
解析
知识点
相似三角形的判定
1
题型:填空题
|
如图3,










两点,已知


正确答案
解析
略
知识点
相似三角形的判定相似三角形的性质与圆有关的比例线段
1
题型:填空题
|
如图3,在





正确答案
10
解析
略
知识点
相似三角形的判定相似三角形的性质
1
题型:填空题
|
如图所示,





正确答案
解析
连结



且


知识点
相似三角形的判定相似三角形的性质
下一知识点 : 相似三角形的性质
扫码查看完整答案与解析