- 离散型随机变量及其分布列、均值与方差
- 共221题
19.某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记

(I)求
(II)若要求

(III)以购买易损零件所需费用的期望值为决策依据,在

正确答案
(I)x的取值为16,17,18,19,20,21,22
x的分布列:
知识点
19.某班
(Ⅰ)求

(Ⅱ)数学老师决定从第一组和第五组的学生中随机抽取2名进行交流,求第一组至少有一名学生被抽到的概率;
(III)设从第一组或第五组中任意抽取的两名学生的数学测试成绩分别记为

正确答案
(1)


解析
试题分析:本题属频率分布表和古典概型,(1)直接按照步骤来求,根据频率相加等于1;(2)利用古典概型公式来计算;(3)利用古典概型公式来计算.
(Ⅰ)

(Ⅱ)设第5组的3名学生分别为

则从5名学生中抽取两位学生有:
其中第一组的2位学生

所以第一组至少有一名学生被老师抽到的概率为
(III)第1组





使

所以


考查方向
解题思路
本题考频率分布表和古典概型,解题步骤如下:(1)直接按照步骤来求,根据频率相加等于1;(2)利用古典概型公式来计算;(3)利用古典概型公式来计算。
易错点
列举事件的时候容易重复或者遗漏。
知识点
14.随机变量ξ的概率分布列为P(ξ=n)=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.在某次考试中,全部考生参加了“科目一”和“科目二”两个科目的考试,每科成绩分为

(1)分别求该考场的考生中“科目一”和“科目二”成绩为
(2)已知在该考场的考生中,恰有2人的两科成绩均为




正确答案
见解析
解析
(1)该考场考生“科目一”科目中
1-0.2-0.375-0.25-0.075=0.1
所以该考场人数为
于是“科目一”考试成绩为
“科目二”考试成绩为

(2)因为两科考试中,共有6人次得分等级为



随机变量
所以

考查方向
解题思路
根据所有可能情况列举出来求解,写出当随机变量取不同值时的情况。
易错点
求期望错误,分布列考虑问题不全
知识点
受轿车在保修期内维修费等因素的影响,企业产生每辆轿车的利润与该轿车首次出现故障的时间有关,某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年,现从该厂已售出的两种品牌轿车中随机抽取50辆,统计数据如下:
将频率视为概率,解答下列问题:
(1)从该厂生产的甲品牌轿车中随机抽取一辆,求首次出现故障发生在保修期内的概率;
(2)若该厂生产的轿车均能售出,记住生产一辆甲品牌轿车的利润为X1,生产一辆乙品牌轿车的利润为X2,分别求X1,X2的分布列;
(3)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌轿车,若从经济效益的角度考虑,你认为应该产生哪种品牌的轿车?说明理由。
正确答案
见解析
解析
(1)设“甲品牌轿车首次出现故障发生在保修期内”为事件A,则P(A)=
(2)依题意得,
X1的分布列为
X2的分布列为
(3)由(2)得E(X1)=1×


E(X2)=1.8×

∵E(X1)>E(X2),
∴应生产甲品牌轿车。
知识点
知离散型随机变量x的分布列如右表。若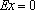
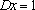
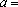
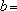
正确答案
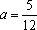

解析
由题知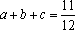
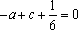
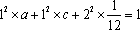
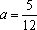
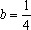
知识点
通过随机询

由
参照右上附表,得到的正确结论( )
正确答案
解析
略
知识点
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物. PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米
石景山古城地区2013年2月6日至15日每天的PM2.5监测数据如茎叶图所示。
(1)小陈在此期间的某天曾经来此地旅游,求当天PM2.5日均监测数据未超标的概率;
(2)小王在此期间也有两天经过此地,这两天此地PM2.5监测数据均未超标.请计算出这两天空气质量恰好有一天为一级的概率;
(3)从所给10天的数据中任意抽取三天数据,记

正确答案
见解析
解析
(1)记“当天PM2.5日均监测数据未超标”为事件A,

(2)记“这两天此地PM2.5监测数据均未超标且空气质量恰好有一天为一级” 为事件B, 
(3)





其分布列为:

知识点
某工厂生产甲、乙两种产品,甲产品的一等品率为80%,二等品率为20%;乙产品的一等品率为90%,二等品率为10%。生产1件甲产品,若是一等品则获得利润4万元,若是二等品则亏损1万元;生产1件乙产品,若是一等品则获得利润6万元,若是二等品则亏损2万元。设生产各种产品相互独立。
(1)记X(单位:万元)为生产1件甲产品和1件乙产品可获得的总利润,求X的分布列;
(2)求生产4件甲产品所获得的利润不少于10万元的概率。
正确答案
见解析。
解析
(1)由题设知,X的可能取值为10,5,2,-3,且
P(X=10)=0.8×0.9=0.72, P(X=5)=0.2×0.9=0.18,
P(X=2)=0.8×0.1=0.08, P(X=-3)=0.2×0.1=0.02。
由此得X的分布列为:
(2)设生产的4件甲产品中一等品有

由题设知

又


所求概率为
答:生产4件甲产品所获得的利润不少于10万元的概率为0.8192。
知识点
一个均匀的正四面体骰子的四个面上分别标有数字l,2,3,4,现将这颗骰子随机抛掷两次,底面上数字分别为 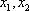
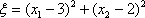
(1)分别求出 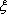
(2)求出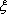
正确答案
见解析
解析
知识点
扫码查看完整答案与解析