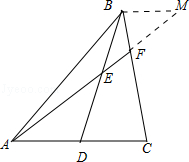- 直线和圆的方程
- 共1449题
如图,△













(1)求该几何体中间一个空心球的表面积的大小;
(2)求图中阴影部分绕直线
正确答案
(1)
解析
(1)连接

设

在

所以
所以
(2)





知识点
已知实数


正确答案
解析
由柯西不等式

知识点
如图,平行四边形



则

正确答案
9
解析
显然




知识点
如图,直线










正确答案
解析
略
知识点
在△ BC中,D是边AC的中点,点E在线段BD上,且满足BE=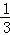
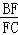
正确答案
解析
如图所示,
过点B作BM∥AC交BF的延长线于点M。
则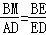
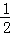
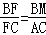
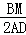
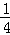
故答案为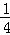
知识点
直线
正确答案
解析
略
知识点
在四棱锥







(1)设平面



(2)求证:

(3)设点





正确答案
见解析
解析
(1)证明: 因为





所以

因为



所以

(2)证明:因为







则



所以 


所以

所以 

因为 




所以 

(3)解:设





所以 
所以 
所以 

所以 
由(2)知平面

因为 
所以 
解得 
所以 
知识点
如图甲,设正方形











(1)证明:

(2)求平面

正确答案
见解析。
解析
(1)证明:在图甲中,易知

因为




(2)解法1、
如图,在图乙中作


由于


所以


所以


图甲中有


设




又由

于是,
在

解法2、
如图,在图乙中作











设





又由

于是,
在
作











显然,

设





设平面







知识点
如图, 





(1)证明: 
(2)求二面角
正确答案
见解析。
解析
(1)
如图所示,取A1B1的中点P,连接MP,NP。
又∵点M,N分别为A1B和B1C1的中点,∴NP∥A1C1,MP∥B1B,
∵NP⊂平面MNP,A1C1⊄平面MNP,∴NP∥平面A1ACC1;
同理MP∥平面A1ACC1;
又MP∩NP=P,
∴平面MNP∥平面A1ACC1;
∴MN∥平面A1ACC1;
(2)侧棱与底面垂直可得A1A⊥AB,A1A⊥AC,及AB⊥AC,可建立如图所示的空间直角坐标系。
则A(0,0,0),B(2,0,0),C(0,2,0),A1(0,0,2),B1(2,0,2),C1(0,2,2),N(1,1,2),M(1,0,1)。
∴


设平面ACM的法向量为

∴
设平面NCM的法向量为

∴
∴



设二面角N﹣MC﹣A为θ,则


故二面角N﹣MC﹣A的正弦值为
知识点
如图,已知四棱锥




点

(1)求证:

(2)求二面角
正确答案
见解析。
解析
(1)证明:
连结
















(2)解法一:










∴

作



所以




在Rt△


∴
∴二面角

解法二:
如图,以点







则


∴
设平面

由

令






∴







∴


∴
∴
∴
∴二面角

知识点
直线

正确答案
解析
略
知识点
直线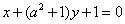
正确答案
解析
略
知识点
极坐标系中,圆ρ=2上的点到直线
正确答案
1
解析
:圆ρ=2 即x2+y2=4,圆心为(0,0),半径等于2.
直线 


圆心到直线的距离等于 
故答案为 1。
知识点
如图,直角梯形
















⑴求证:平面

⑵求直线

正确答案
见解析。
解析
⑴证明:












⑵(方法一)以E为原点,EA、EC分别为





















由⑴知

设直线


则
故求直线


(方法二)作


由⑴知AE






知识点
设地球半径为



正确答案
解析
略
知识点
扫码查看完整答案与解析