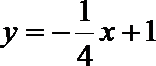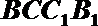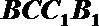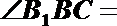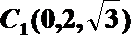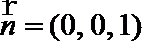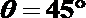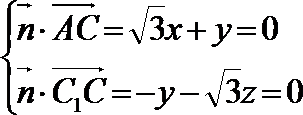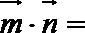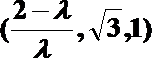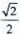- 直线和圆的方程
- 共1449题
11. 已知直线






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 过点A(0,1)作一直线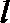
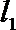


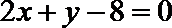

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知椭圆








(2)平面上的点






正确答案
(I)由
设







消去



故椭圆

(II)由


因为




设
设
因为

解得

故所求直线


解析
解析已在路上飞奔,马上就到!
知识点
11.直线


正确答案
(-2,3)
解析
解析已在路上飞奔,马上就到!
知识点
9.若直线2ax-by+2=0 (a >0, b>0) 被圆x2+y2+2x-4y+1=0截得的弦长为4,则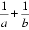
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.直线ax+3y+4=0与直线2x+(a+1)y+1=0平行,则实数a的值是_____.
正确答案
-3或2
解析
解析已在路上飞奔,马上就到!
知识点
10.过点

正确答案
x+y-2=0
解析
解析已在路上飞奔,马上就到!
知识点
16.经济学中的“蛛网理论”(如图),假定某种商品的“需求—价格”函数的图象为直线l1,“供给—价格”函数的图象为直线l2,它们的斜率分别为k1.k2,l1与l2的交点P为“供给—需求”均衡点,在供求两种力量的相互作用下,该商品的价格和产销量,沿平行于坐标轴的“蛛网”路径,箭头所指方向发展变化,最终能否达于均衡点P,与直线l1. l2的斜率满足的条件有关,从下列三个图中可知最终能达于均衡点P的条件为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知直线








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.直线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
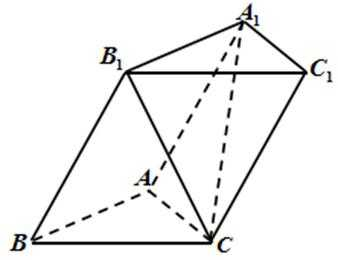
20.如图,三棱柱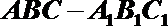
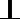
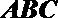
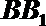
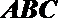
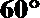
(Ⅰ)求直线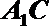
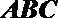
(Ⅱ)在线段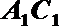
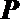
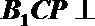
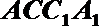
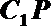
正确答案
解:(Ⅰ)过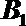

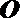
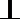
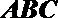
∴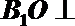
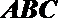
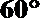
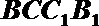
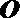
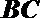
以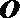
则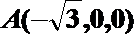
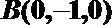
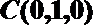


∴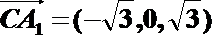
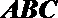
设直线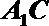
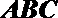
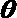
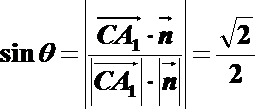
所以,直线

(Ⅱ)假设在线段
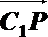

则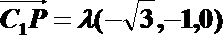
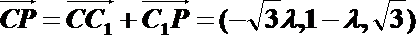
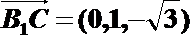
设平面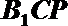

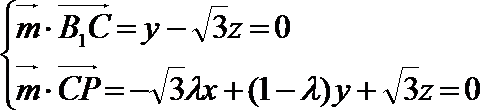
令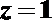
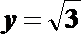
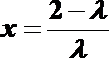
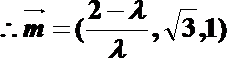
设平面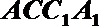

令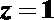
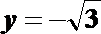
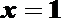

要使平面
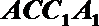
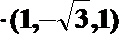


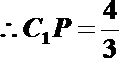
解析
解析已在路上飞奔,马上就到!
知识点
6.若P(2,-1)为圆(x-1)2+y2=25的弦AB的中点,则直线AB的方程是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.过抛物线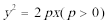
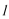

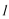
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知两点


① 
② 
③ 
④ 
其中为“和谐直线”的是_________。(请写出符合题意的所有编号)
正确答案
①④
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析