- 直线和圆的方程
- 共1449题
已知:数列




(1)求:

(2)求:数列
(3)若数列






正确答案
见解析
解析
(1) 




(2)


两式相减得
所以


所以数列


所以


(3)
所以

令

①-②得


所以
知识点
如图4,△OAB是等腰三角形,P是底边AB延长线上一点,且
正确答案
解析
略
知识点
将标号为1,2,3,4,5,6的6张卡片放入3个不同的信封中,若每个信封放2张,其中标号为1,2的卡片放入同一信封,则不同的方法共有( )
正确答案
解析
由题意知,本题是一个分步计数问题,
∵先从3个信封中选一个放1,2有3种不同的选法,
再从剩下的4个数中选两个放一个信封有C42=6,
余下放入最后一个信封,
∴共有3C42=18
故选B。
知识点
如图,






(1) 求证:
(2)若




正确答案
见解析
解析
(1)证明:因为
所以
又因为

所以 

因为

所以 
(2)因为△


不防设

又因为



由此以




则有





所以

设平面

则
即
令

所以
又平面

所以 
所以二面角

知识点
已知椭圆






正确答案
解析
设




① ②得
∴













知识点
已知直线




(1)当



(2)过坐标原




正确答案
见解析。
解析
(1)当





联立方程组




另解:



直线



解得

当


当


因此



(2)直线



直线OA的方程为

解得


故当


由

因此P点轨迹的普通方程为
故P点轨迹是圆心为(

知识点
过点(2,1)作圆
正确答案
解析
略
知识点
下列说法正确的个数是
①“在
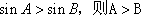
②“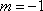
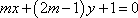
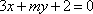
③“三个数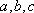
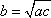
④命题“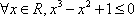
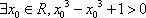
正确答案
解析
略
知识点
若
正确答案
8
解析
略
知识点
设当


正确答案
解析
∵

令





当









知识点
如图,四边形ABCD是边长为2的正方形,MD⊥平面ABCD,NB∥MD,且NB=1,MD=2;
(1)求证:AM∥平面BCN;
(2)求AN与平面MNC所成角的正弦值;
(3)E为直线MN上一点,且平面ADE⊥平面MNC,求
正确答案
见解析
解析
(1)∵ABCD是正方形,
∴BC∥AD.
∵BC平面AMD,AD
∴BC∥平面AMD.
∵NB∥MD,
∵NB平面AMD,MD
∴NB∥平面AMD.
∵NB


∴平面AMD∥平面BCN ………………………………………………………3分
∵AM
∴AM∥平面BCN ……………………………………………………………4分
(也可建立直角坐标系,证明AM垂直平面BCN的法向量,酌情给分)
(2)
则






设平面MNC的法向量
则


设AN与平面MNC所成角为

(3)设


又




欲使平面ADE⊥平面MNC,只要




知识点
如图, 




(1)求证:
(2) 求二面角
(3)设点




正确答案
见解析
解析
(1)证明: 因为

所以
因为
所以
所以

从而 
(2)解:因为
所以建立空间直角坐标系
设

则





所以

设平面



令

因为




所以
因为二面角为锐角,所以二面角

(3)解:点


则
因为

所以
即

此时,点


知识点
在等腰梯形ABCD中,




(1)求证:

(2)求证:

(3)求二面角
正确答案
见解析
解析
(1)证明:因为
所以
所以四边形
又因为等腰梯形,
所以 

所以
由已知可知 平面

因为 平面
所以

(2)证明:因为

所以平面
又因为

所以 

(3)因为
同理

设
则



则
设平面



得 
因为


又

所以


所以平面

所以
由图形可知二面角
所以二面角

知识点
如图(1),等腰直角三角形








(1)求证:
(2)若




正确答案
见解析
解析
(1)证明:







(2)解:




坐标系(如图),……………………………5分





设面










解得:



知识点
等边三角形ABC的边长为3,点D、E分别是边AB、AC上的点,且满足
(1)求证:A1D丄平面BCED;
(2)在线段BC上是否存在点P,使直线PA1与平面A1BD所成的角为600?若存在,求出PB的长;若不存在,请说明理由。
正确答案
见解析。
解析
(1)∵ 正 △ ABC的边长为3,且

∴ AD=1,AE=2,
△ ADE中,∠ DAE=60°,由余弦定理,得
DE=
∵ AD2+DE2=4=AE2,∴ AD⊥DE。
折叠后,仍有A1D⊥DE
∵ 二面角A1﹣DE﹣B成直二面角,∴ 平面A1DE⊥平面BCDE
又∵ 平面A1DE∩平面BCDE=DE,A1D⊂平面A1DE,A1D⊥DE
∴ A1D丄平面BCED;
(2)假设在线段BC上存在点P,使直线PA1与平面A1BD所成的角为60°
如图,作PH⊥BD于点H,连接A1H、A1P
由(1)得A1D丄平面BCED,而PH⊂平面BCED
所以A1D丄PH
∵ A1D、BD是平面A1BD内的相交直线,
∴ PH⊥平面A1BD
由此可得∠ PA1H是直线PA1与平面A1BD所成的角,即∠ PA1H=60°
设PB=x(0≤x≤3),则BH=PBcos60°=

在Rt△PA1H中,∠PA1H=60°,所以A1H=
在Rt△DA1H中,A1D=1,DH=2﹣
由A1D2+DH2=A1H2,得12+(2﹣

解之得x=
所以在线段BC上存在点P,使直线PA1与平面A1BD所成的角为60°,此时PB=
知识点
扫码查看完整答案与解析




























































