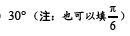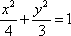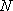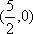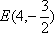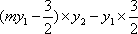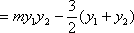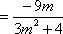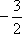- 直线和圆的方程
- 共1449题
在平面直角坐标系内,动圆


(1)求动圆圆心

(2)中心在











正确答案
见解析。
解析
由题可知,圆心


由抛物线定义知,



(确定“曲线是抛物线”1分,说明抛物线特征1分)
所以动圆圆心


⑵解法1、
设







将其代入抛物线方程,得:

联立 

由

注意到



因此,椭圆


解法2、
设



即
即





联立 

由

注意到



因此,椭圆


知识点
如图,圆







正确答案
4,
解析
略
知识点
在平面直角坐标系




(1)求动点
(2)设直线











正确答案
(1)
(2)存在点
解析
(1)解:设点

由题意知
化简得
所以动点

(2)设直线

因为



所以有
由



由(1)(2)(3)得
所以 存在点

知识点
正方体









正确答案
解析
略
知识点
在极坐标系中,圆

正确答案
解析
略
知识点
如图,
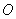
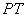
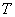
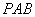
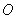
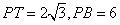
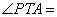
正确答案
解析
略
知识点
已知动点


(1)求动点

(2)若直线



(3)在(2)的条件下,求弦长
正确答案
见解析。
解析
知识点
已知动点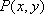
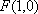
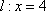

(1)求动点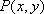
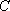
(2)已知直线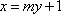
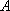
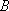
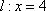
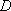
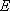
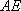
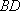
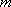
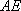
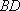
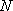
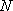
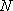
正确答案
(1)
(2)直线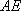
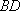
解析
(1)由题意得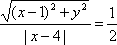
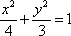
所以动点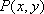
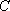
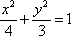
(2)当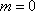
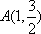
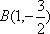
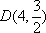
直线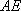
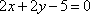
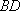
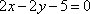
方程联立解得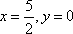
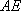
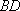
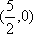
假设直线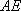
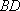
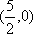
证明:设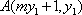
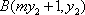
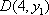
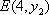
由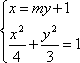

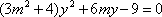
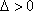
由韦达定理得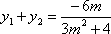
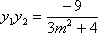
因为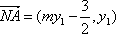
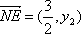
所以
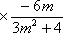
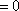
所以,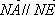
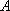
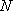
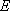
同理可证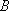
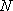
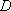
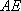
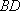
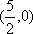
知识点
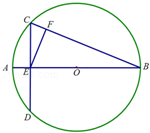
如图,在圆O中,直径AB与弦CD垂直,垂足为E(E在A,O之间),EF⊥BC,垂足为F,若,则AB=6,CF•CB=5,则AE= 。
正确答案
1
解析
解:在Rt△BCE中,EC2=CF•CB=5,∴EC2=5。
∵AB⊥CD,∴CE=ED。
由相交弦定理可得AE•EB=CE•EB=CE2=5。
∴(3﹣OE)•(3+OE)=5,解得OE=2,∴AE=3﹣OE=1。
故答案为1。
知识点
经过点F (0,1)且与直线y=﹣1相切的动圆的圆心轨迹为M点A、D在轨迹M上,且关于y轴对称,过线段AD (两端点除外)上的任意一点作直线l,使直线l与轨迹M 在点D处的切线平行,设直线l与轨迹M交于点B、C。
(1)求轨迹M的方程;
(2)证明:∠BAD=∠CAD;
(3)若点D到直线AB的距离等于
正确答案
见解析。
解析
(1)设圆心坐标为(x,y),由题意动圆经过定点F(0,1),且与定直线:y=﹣1相切,
所以 
即(y﹣1)2+x2=(y+1)2,
即x2=4y,故轨迹M的方程为x2=4y。
(2)由(1)得y=

设D(x0,

则A(﹣x0,


则kBC=


kAC=


∴kBC+AB=


∴∠BAD=∠CAD。
(3)点D到直线AB的距离等于
不妨设C在AD上方,即x2<x1,直线AB的方程为:y﹣
解得B点的坐标为(x0﹣4,


由(2)知,∠CAD=∠BAD=45°,同理可得|AC|=2
∴△ABC的面积为


解得x0=±3。
当x0=3时,B((﹣1,

当x0=﹣3时,B((﹣7,

知识点
已知圆C经过直线2x﹣y+2=0与坐标轴的两个交点,又经过抛物线y2=8x的焦点,则圆C的方程为 。
正确答案
解析
抛物线y2=8x的焦点为F(2,0),直线2x﹣y+2=0与坐标轴的两个交点坐标分别为A(﹣1,0),B(0,2),
设所求圆的方程为x2+y2+Dx+Ey+F=0。
将A、B、F三点的坐标代入圆的方程得:
解得
于是所求圆的方程为x2+y2﹣x﹣y﹣2=0。
即
故答案为:
知识点
已知点P是圆F1:
(1)求点M的轨迹C的方程;
(2)设轨迹C与x轴的两个左右交点分别为A,B,点K是轨迹C上异于A,B的任意一点,KH⊥x轴,H为垂足,延长HK到点Q使得HK=KQ,连结AQ延长交过B且垂直于x轴的直线l于点D,N为DB的中点,试判断直线QN与以AB为直径的圆O的位置关系。
正确答案
见解析。
解析
(1)由题意得,
圆
从而
∴ 点M的轨迹是以


则短半轴
椭圆方程为:
(2)设

∵

∴




又


令

又



∴

∴

∴


知识点
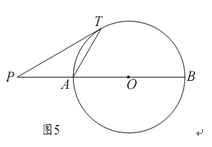
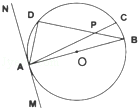
如图,半径是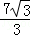
正确答案
4
解析
∵MN切圆O于A,∴∠B=∠DAN=30°,
∵AB是直径,可得∠ADB=90°,
∴AD=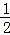
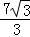
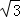
又∵圆O中,PB×PD=CP×PA=12
∴设PD=x,可得x(7﹣x)=12,解之得x=3或4
∵PD>PB,∴PD=4(﹣3舍去)
故答案为:4
知识点
如图,已知椭圆


(1)求椭圆的标准方程;
(2)设P是椭圆上异于A、B的任意一点,PH⊥x轴,H为垂足,延长HP到点Q使得HP=PQ,连接AQ并延长交直线l于点M,N为MB的中点,判定直线QN与以AB为直径的圆O的位置关系。
正确答案
见解析。
解析
(1)易知A(﹣a,0),B(a,0),F1(﹣c,0),
∴
又

∴
(2)设P(x0,y0),则Q(x0,2y0)(x0≠±2),
∴

∴

∴
又点P的坐标满足椭圆方程,则
所以 

∴直线QN的方程:
化简整理得到:
所以点O到直线QN的距离
故直线QN与AB为直径的圆O相切。
知识点
在平面斜坐标系












正确答案
解析
略
知识点
扫码查看完整答案与解析