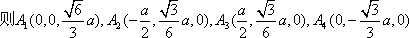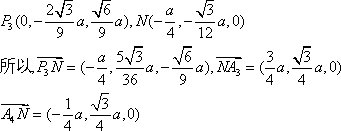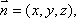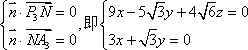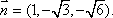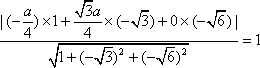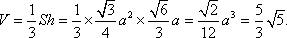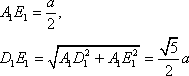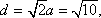- 棱柱、棱锥、棱台的体积
- 共114题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
如图,在四面体







(1)若



(2)若二面角





正确答案
见解析
解析
(1)如图所示,设F为AC的中点,由于AD=CD,所以DF⊥AC.
故由平面







故四面体ABCD的体积
(2)如图所示设G、H分别为变CD,BD的中点,则FG//AD,GH//BC,,从而


设E为边AB的中点,则EF//BC,由











在

从而
因





故异面直线

知识点
如图13,四棱锥PABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点。
正确答案
见解析。
解析
(1)证明:连接BD交AC于点O,连接EO.
因为ABCD为矩形,所以O为BD的中点。
又E为PD的中点,所以EO∥PB.
因为EO⊂平面AEC,PB⊄平面AEC,
所以PB∥平面AEC.
(2)
因为PA⊥平面ABCD,ABCD为矩形,
所以AB,AD,AP两两垂直。
知识点
(1)如图,对于任一给定的四面体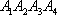
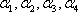
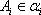
(2)给定依次排列的四个相互平行的平面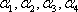
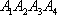
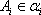
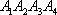
正确答案
见解析
解析
(1)如图所示,取A1A4的三等分点P2,P3,A1A3的中点M,A2A4的中点N,
过三点A2,P2,M作平面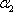
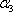
因为A2P2//NP3,A3P3//MP2,所以平面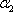
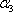
再过点A1,A4分别作平面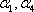
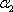
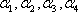
由线段A1A4被平行平面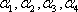
故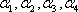
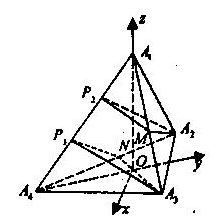
(2)解法一:当(1)中的四面体为正四面体,若所得的四个平行平面,每相邻两平面之间的距离为1,则正四面体A1A2A3A4就是满足题意的正四面体,设正四面体的棱长为a,以△A2A3A4的中心O为坐标原点,以直线A4O为y轴,直线OA1为z轴建立如图的右手直角坐标系,
令P2,P3为A1A4的三等分点,N为A2A4的中点,有
设平面A3P3N的法向量
有
所以,
因为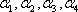
解得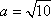
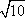
所以所求正四面体的体积
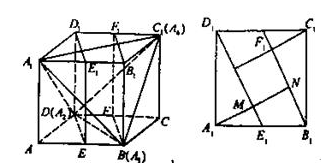
解法二:如图,现将此正四面体A1A2A3A4置于一个正方体ABCD—A1B1C1D1中,(或者说,在正四面体的四个面外侧各镶嵌一个直角三棱锥,得到一个正方体),E1,F1分别是A1B1,C1D1的中点,EE1D1D和BB1F1F是两个平行平面,若其距离为1,则四面体A1A2A3A4即为满足条件的正四面体。右图是正方体的上底面,现设正方体的棱长为a,若A1M=MN=1,则有
据A1D1×A1E1=A1M×D1E1,得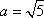
于是正四面体的棱长
其体积
(即等于一个棱长为a的正方体割去四个直角正三棱锥后的体积)
知识点
如图11,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm,高为6 cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )
正确答案
解析
知识点
扫码查看完整答案与解析